Pascal’s law, also known as the principle of transmission of fluid pressure or Pascal’s Principle is a very important theory of fluid mechanics. The law was first stated by the French Mathematician and Physicist Blaise Pascal in 1653 and as per his name, this principle is known as Pascal’s law or Pascal’s Principle. In this article, we will explore details about Pascal’s Law, its formula, equation, applications, and examples.
What is Pascal’s law?
Pascal’s law in fluid mechanics states that a change in pressure at any point in a confined incompressible static fluid is transmitted evenly throughout the liquid in all directions.
The pressure remains constant and is transmitted equally to all parts and acts at the right angle to the wall of the enclosure. As pressure remains constant and Force=Pressure X Area; So, the force applied is proportional to the surface area. So, with an increase in surface area, the force will increase as pressure is constant.
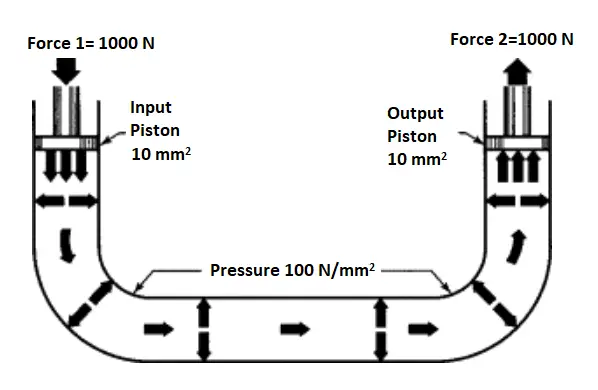
As can be seen in Fig. 1, the pressure generated due to applied force 1 (1000 N) is constant throughout (100 N/mm2). Also, Force 2 is the same as force 1 as the area of the output piston is equal to the input piston. If the area of the 2nd piston is 5 times that of the 1st piston, the force at the 2nd piston will be 5 times of the 1st piston. Note that, the pressure transmitted does not depend on the shape of the container.
Pascal’s law is the origin of many inventions used in our day-to-day life such as hydraulic brakes and lifts.
Pascal’s Law Formula / Pascal’s Law Equation
Let’s understand the above concept of Pascal’s law using mathematical equations. Refer to the Fig. 2 given below:
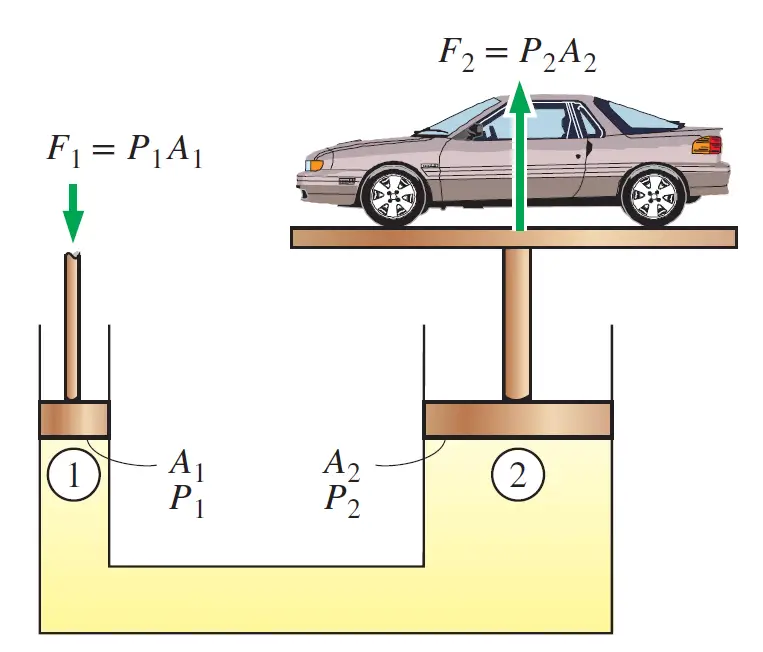
The above image (Fig. 2) explains the principle of the hydraulic jack. You might have seen in car garages that to lift a heavy car, a small force is applied. This is one of the best examples of Pascal’s law.
In Fig. 2, there are two pistons; Piston 1 and Piston 2. Force F1 is applied at Piston 1. So generated Pressure in the fluid medium of the container is, P1=F1/A1 (A1=Area of Piston 1). As per Pascal’s law, the same pressure will be transmitted throughout the container and will exert at Piston 2.
So, Pressure at Piston 2, P2=P1.
Or, F1/A1=F2/A2 (A2=Area of Piston 2)
Or, F2=F1 X (A2/A1)
Since A2>A1; F2>F1
This area ratio A2/A1 is called the ideal mechanical advantage of the hydraulic lift. So you can see that by using a hydraulic jack area ratio of 200 one can easily lift a weight of 2000 Kg by applying a force of only 10 Kg.
Examples of Pascal’s Law /Application of Pascal’s Law
Using Pascal’s Law various pieces of equipment are manufactured which are used in day-to-day life. A few examples of the application of Pascal’s Law are listed below:
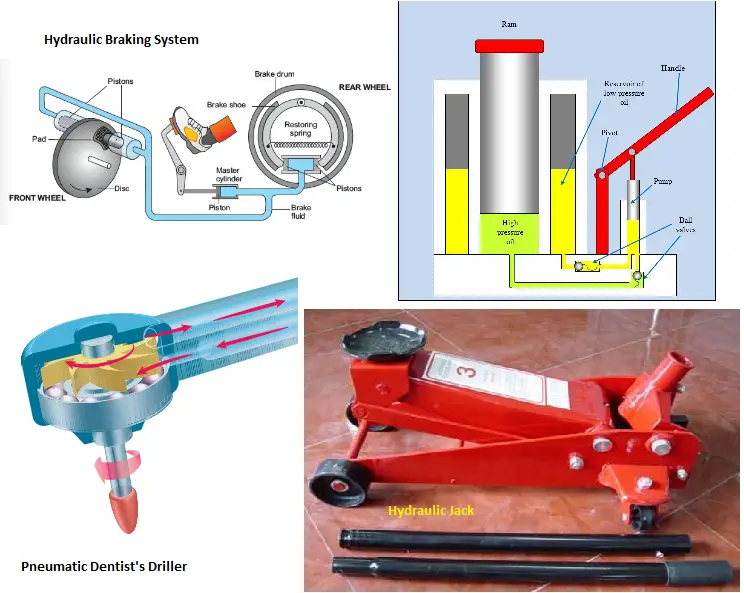
- Hydraulic jack and hydraulic press.
- Hydraulic Brakes for increasing resisting force in the vehicle braking systems.
- Artesian wells, water towers, and dams.
- Aircraft Hydraulic System: Hydraulic power systems in Aircraft use Pascal’s law to slow down aeroplanes on the runway. Also, used in flight control mechanisms, landing gears, etc.
- Hydraulic Pumps: Hydraulic Pumps used in the Automobile industry uses the philosophy of Pascal’s Law.
- Wide applications of Pascal’s law are also seen in hydraulic testing of pressurized tanks, calibration of pressure gages, pressing of oils such as olive, hazelnut, and sunflower oils, compression of wood stocks, etc.
- Various Pneumatic devices like Dentists’ drills, jackhammers, paint sprayers, and air brakes on trucks, etc work on the principle of Pascal’s Law.

Nice written sir. Good explanation.
Great explanation. Thank you.
Thank you very much. I’m not an Engineer. Rather, I’m a Geographer. But I have lot of interest in Mechanical Engineering topics. Now, I am working with a project of Concentrated Solar Power (CSP). Here, I need to know about Pascal’s Law, that is to be applied as a part of Mechanical Component in my Project. Your post has heled me a lot. If you feel free, I would like to consult with you in time, as a favor from your side. Thanking you again.
thank ypu this has been very helpful