Some users of START-PROF Piping Stress Analysis software ask the same question:
Why loads and displacements are not zero in a cold state?
I will try to explain this phenomenon in this article.
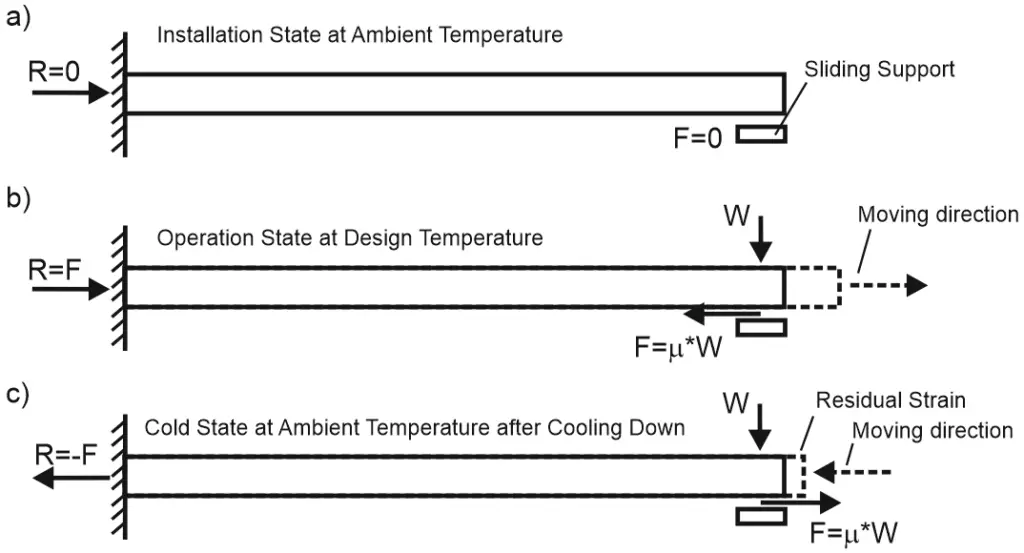
Let’s imagine the simple piping model – console pipe. Anchor on the left end and free end with sliding support at the right.

In installation state (a) at ambient temperature friction forced doesn’t exist because there are no displacements. The anchor load R is zero.
In operation state (b) pipe elongates and the right end slides in the right direction. The friction force is always directed in the opposite direction of movement. Therefore friction force direction is from right to left. The friction force value is F= µ *W, where W is the support load from the weight load, and µ is the friction factor. The anchor load is R=F.
Will friction force and support load R exist in a cold state (c) or not? The answer is yes! The right end of the pipe will slide to the left direction during cooling down. The friction force will change its direction to the right. When the pipe will reach the ambient temperature friction force will not disappear. The anchor load will be R=-F. The effect of friction forces in cold conditions looks like the cold spring effect. The pipe remains under tension, support loads are not zero.
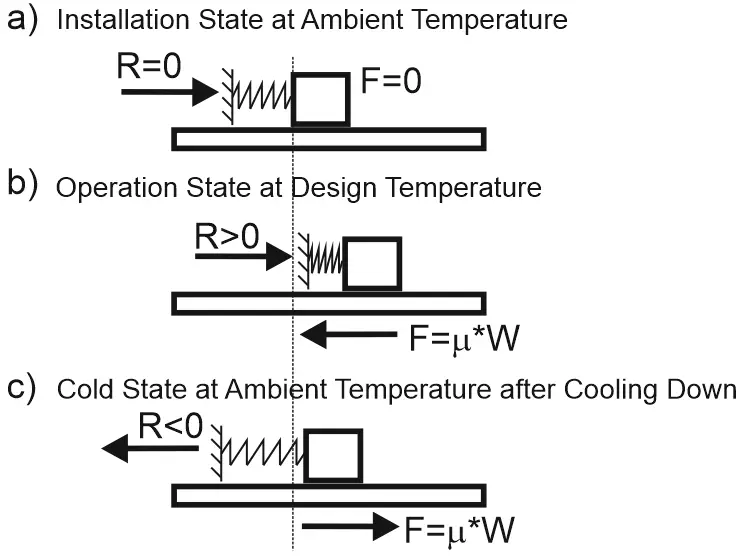
This phenomenon can also be illustrated using the heavy brick and spring. We push the brick in the right direction (b) and then pull it back into the left direction (c). The spring in cold conditions (c) will remain stretched. Reaction force R will be not zero.
Should we consider this effect during pipe stress analysis calculations? Yes!
Usually, when engineers perform pipe stress analysis, the friction forces in the cold state are assumed to be zero. The following load cases can be created:
L1: W+P SUS
L2: W+P+T OPE
L3: L2-T COLD (follow up L2)
L4: L2-L1 EXP
L5: L2-L3 EXP
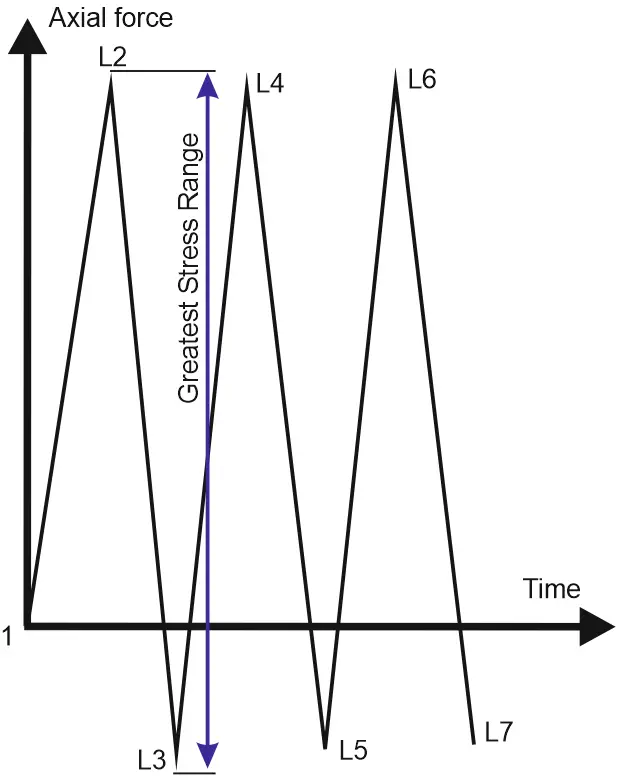
Usually, we calculate the expansion stress range L4 between the operation condition (L2) and installation condition (L1). But what if we will calculate the expansion stress range (L5) between the operation condition (L2) and cold condition (L3)? Will it be greater or lower?
In operating condition L2, the stress due to friction is compressive S=-F/A.
In installation condition L1, the stress is zero S=0.
In cold condition L3 the stress is tensile S=+F/A.
This means that L4 expansion range will give SA=ABS(-F)/A=F/A, but L5 expansion range will give SA=ABS(-F+F)/A=2*F/A.
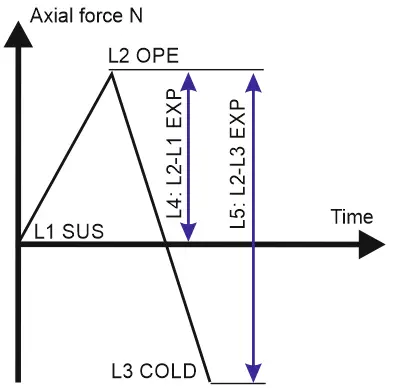
Expansion range L5 is 2 times greater than L4! It’s more correct to calculate the expansion range between the operation and cold state (L2-L3) with friction instead of the operation state and installation state without friction (L2-L1).
Friction factor decrease after several movements. Thus sometimes friction factor for L5 stress range calculation is required to be decreased by 1/2 from the full value. For example, if the friction factor for the L2 load case is µ =0.3, then for L3 we should use µ =0.3*0.5=0.15. In this case, the stress range L5 will be SA=ABS(-F+0.5F)/A=1.5*F/A.
How to model it in START-PROF?
Let’s check how to calculate this in PASS/START-PROF software.
Create a new simple model, pipe with an anchor on the left end and sliding support with a heavy valve on another end.
Modeling the cold state with friction is a standard function of the START-PROF operation mode editor.
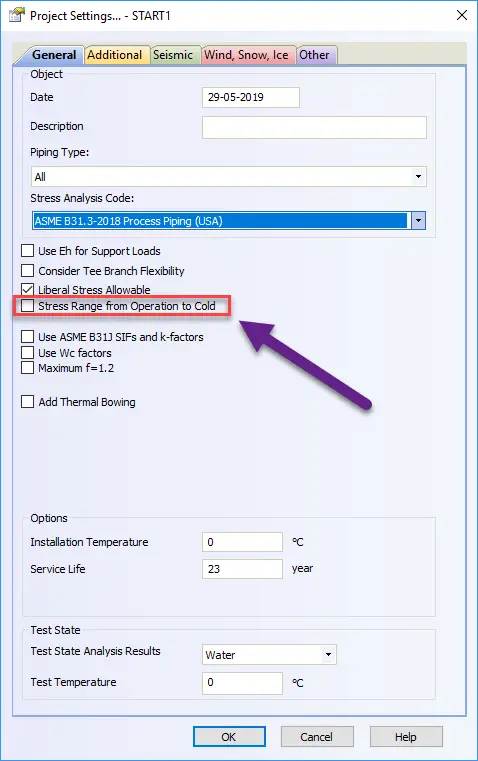
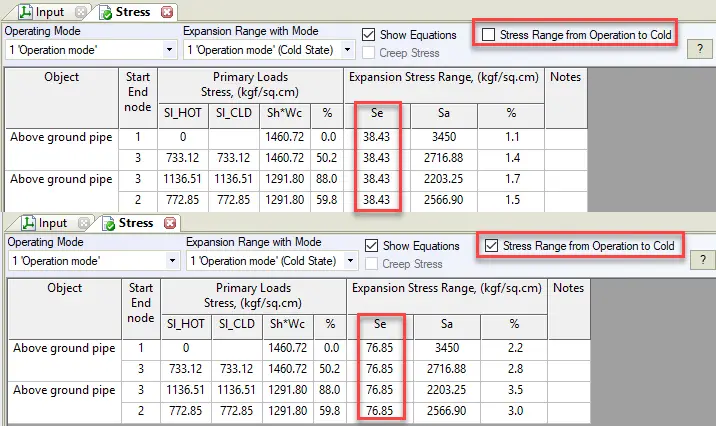
If the option “Stress Rang from Operation to Cold” is turned off, START-PROF will calculate stress range L4 (between operation L2 and installation L1). If we turn on this option, START-PROF will calculate stress range L5 (between operation L2 and cold L3) considering the backward friction effect.
In the stress table we can see, that the stress range is 2 times greater for stress range operation-cold L5 than for operation-installation L4.
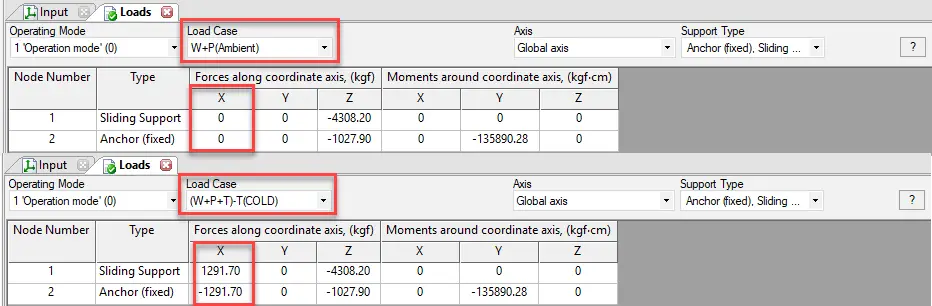
Let’s compare support loads in Installation state L1 and Cold state L3. In the installation state, the support load in the X direction is zero. But in a cold state, it is not zero and equal to the friction force on sliding support.
In some cases, the friction effect may give even greater nozzle loads in a cold state than in a hot state.
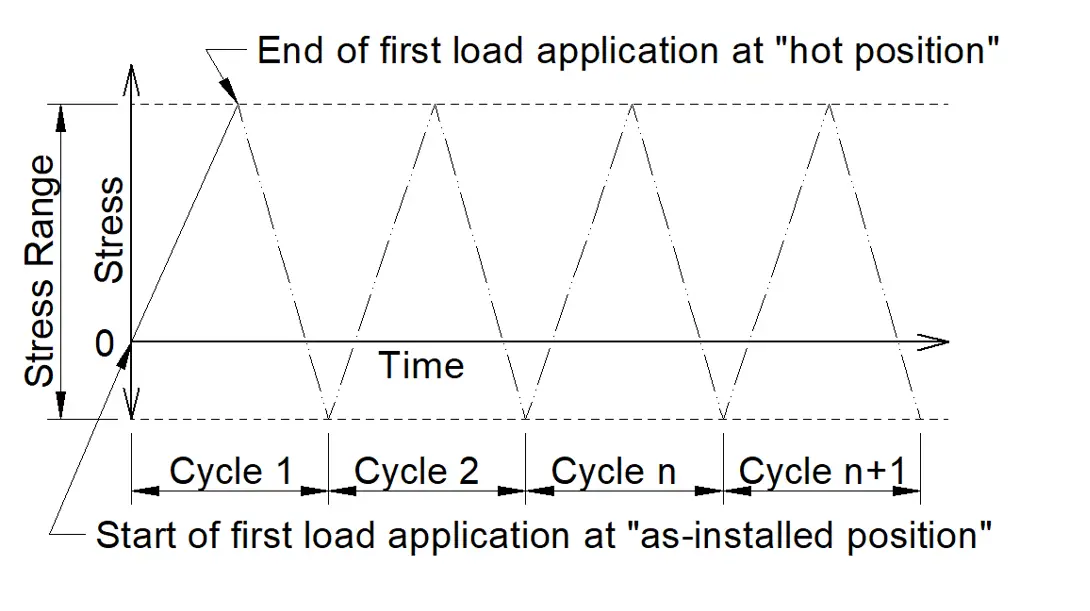
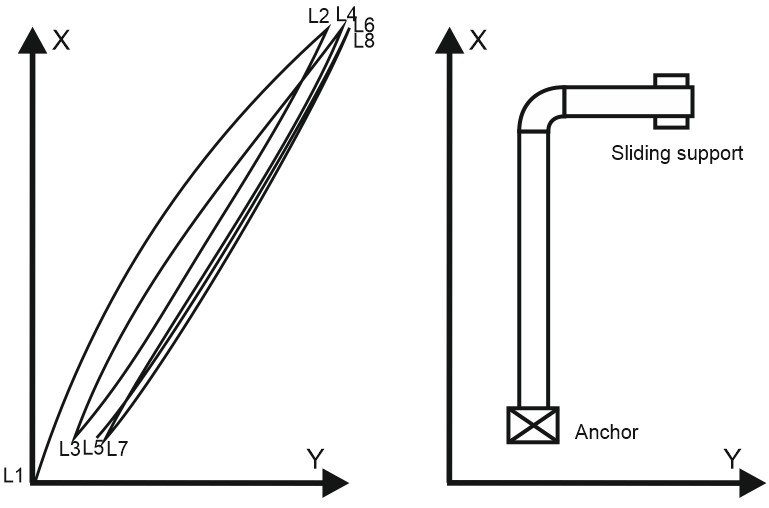
After the second heating of the complex piping system, the displacements will be slightly different from the displacements during the first heating up. The same situation with second, third, etc. cycles.
What if we have several warming and cooling cycles?
Let’s imagine that we have several heating and cooling cycles
L1: W+P SUS
L2: W+P+T OPE
L3: L2-T COLD (following up L2)
L4: L3+T OPE (following up L3)
L5: L2-T COLD (following up L4)
L6: L3+T OPE (following up L5)
L7: L2-T COLD (following up L6)
L8: L3+T OPE (following up L7)
…
For the L-shape piping model, the sliding support displacements diagram in the XY plane has the following shape:
The greatest loads will be at the first cycle L2-L3. The greatest stress range will be L2-L3. The L1-L2 range is not the greatest.