Moment of Inertia: Introduction, Definition, Formula, Units, Applications

Moment of Inertia is a very useful term for mechanical engineering and piping stress analysis. It represents the rotational inertia of an object. The moment of inertia signifies how difficult is to rotate an object. In this article, we will explore more about the Moment of Inertia, Its definition, formulas, units, equations, and applications.

What is Moment of Inertia?

There are two types of moment of inertia; the mass moment of inertia and the area moment of inertia.

The moment of inertia of a Mass (I) is defined as the sum of the products of the mass (m) of each particle of the body and the square of its perpendicular distance (r) from the axis and is mathematically represented as

I = mr²

The mass distribution of a body of rotating particles from the axis of rotation is represented by the moment of inertia. The value of the moment of inertia is independent of the forces involved and depends only on the body geometry and position from the axis of rotation. The mass moment of inertia for rotation is analogous to mass in linear movement. So, the mass moment of inertia for rotation is treated the same way as the mass in linear motion with features like

• The angular momentum of a body is given by I.ω. Newton’s Second Law of Motion, when applied to rotating bodies, states that the torque is directly proportional to the rate of change of angular momentum.
• When a body with the mass moment of inertia (I) is rotated about any given axis, with an angular velocity ω, then it possesses some kinetic energy of rotation given by = 1/2 Iω²

The moment of Inertia of an Area (I) represents the distribution of points in a cross-sectional area with respect to an axis. It is also known as the second moment of area. For an elemental area dA in the XY plane, the area moment of inertia is mathematically defined as I_x and I_y as shown in Fig. 1 below.

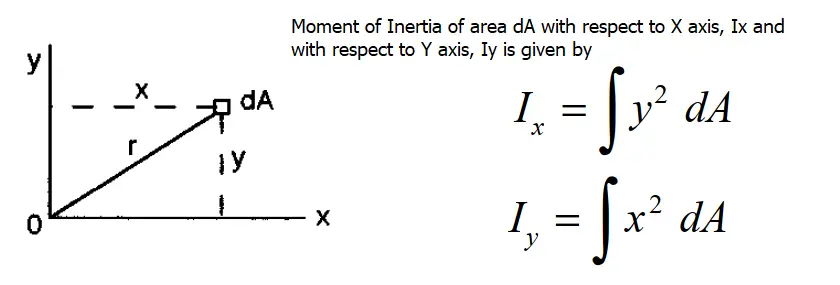
The Formula for Moment of Inertia

In beam theory, the formula of the moment of inertia is very important. Depending on the cross-section of the object the equation of the moment of inertia varies. Note that, the moment of inertia is always positive. In this section, we will find out the moment of inertia formula for a few common geometrical cross sections.

Moment of Inertia Formula for Square Cross-Section:

The moment of inertia equation for a square is given by I_x=I_y= a⁴/12 where a=length of side.

The Equation for Moment of Inertia for Circular Cross Section:

The moment of inertia for a circular cross-section is given by I=πd⁴/64 where d=Diameter of the circle. In a similar way, the moment of area of a pipe is given by I=π(D⁴-d⁴)/64 Where D=Pipe OD and d=Pipe ID.

The following image provides the area moment of inertia formula for some more common shapes.

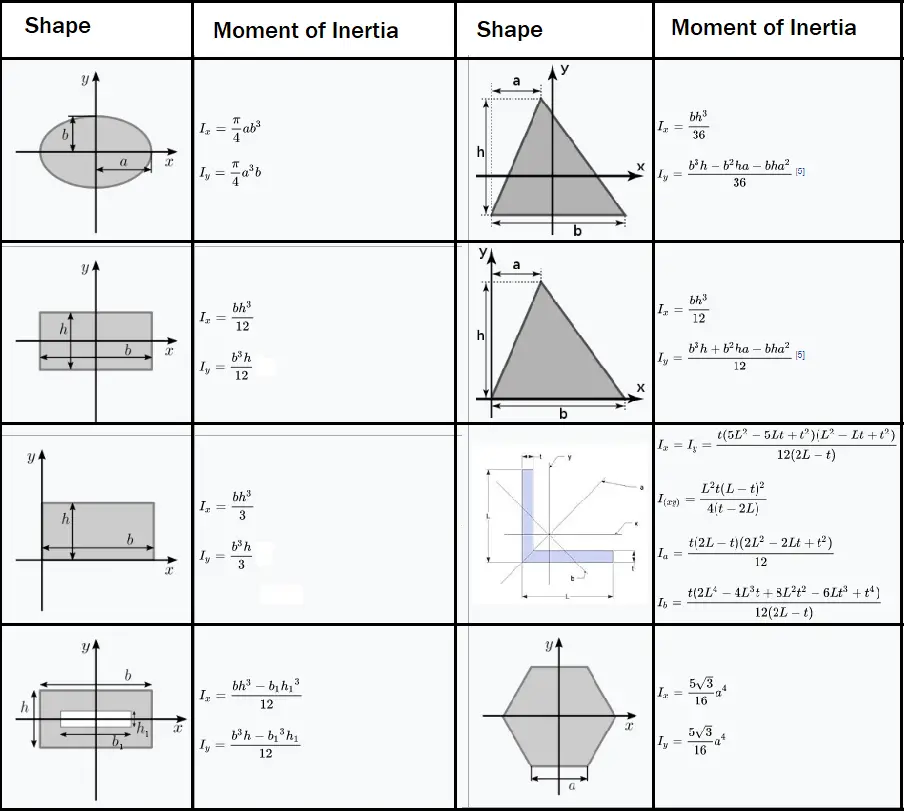
Units of Moment of Inertia

The unit of mass moment of inertia in the SI unit system is kg.m2 and in the FPS unit system is lbf·ft·s²

The unit of an area moment of inertia in the SI unit is m4 and in the FPS unit system is inches⁴.

Polar Moment of Inertia

The polar moment of inertia is defined with respect to an axis perpendicular to the area considered. It provides a beam’s ability to resist torsion or twisting. The polar moment of inertia (J) of a circular area is given by J=πd⁴/32.

Applications of Moment of Inertia

• Mass moment of inertia provides a measure of an object’s resistance to change in the rotation direction.
• Area moment of inertia is the property of a geometrical shape that helps in the calculation of stresses, bending, and deflection in beams.
• A polar moment of inertia is required in the calculation of shear stresses subject to twisting or torque.
• The moment of inertia “I” is a very important term in the calculation of Critical load in Euler’s buckling equation. The Critical Axial load, Pcr is given as P_cr=π²EI/L².
• A moment of inertia is required to calculate the Section Modulus of any cross-section which is further required for calculating the bending stress of a beam. Bending stresses are inversely proportional to the Moment of Inertia. The larger the moment of inertia, the greater is the moment of resistance against bending.

Section Modulus

The section modulus of a section is defined as the ratio of the moment of inertia (I) to the distance (y) of extreme fiber from the neutral axis in that section. Section modulus is denoted by “Z” and mathematically expressed as

Z=I/y

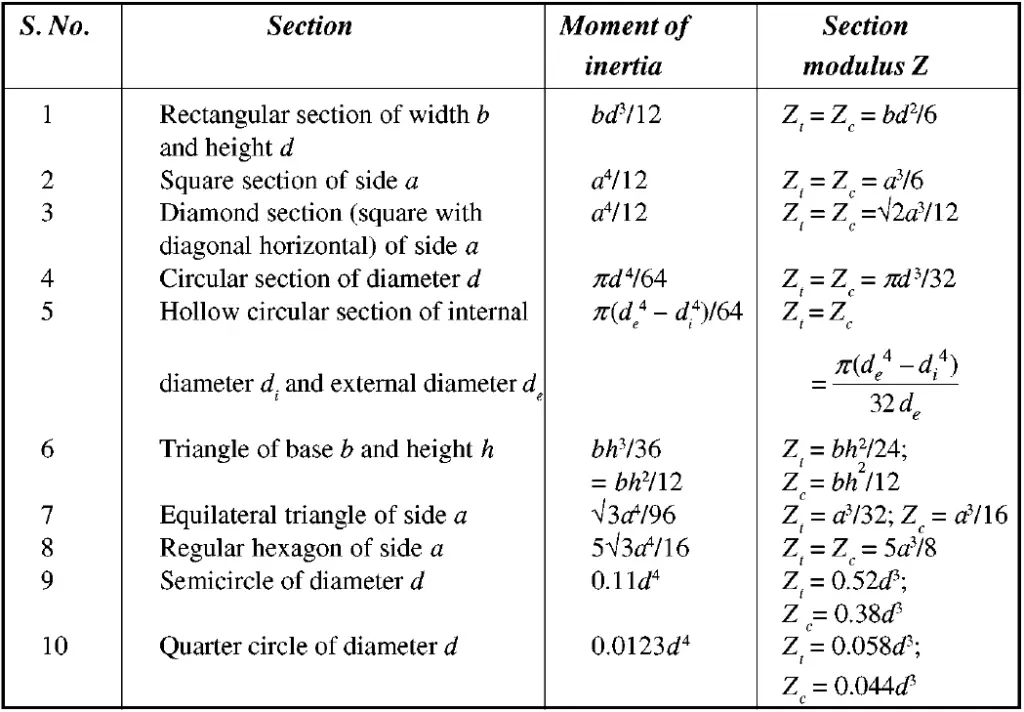
In SI unit systems the unit of Section Modulus is m³ and in the US unit system inches³. The table provided in Fig. 3 provides the moment of inertia and section modulus formula for common geometrical shapes. (Here, Z_c and Z_t are the section moduli in compression and tension)