Variable Spring Support Design without the aid of Caesar II Hanger Auxiliary

Variable Spring Hanger Supports are widely used in critical pipe systems for their load-bearing capability allowing thermal movements. In Caesar II, We can easily design a variable spring hanger support by double-clicking the checkbox for the hanger auxiliary. The software follows the below-mentioned steps to select its spring.

• CAESAR II puts rigid support at the hanger location and does a weight analysis to find out the weight that the support should carry. This load is used as the Hot Load (HL).
• CAESAR II applies a force equal to that Hot Load (but not stiffness (k)) at the hanger location and then runs an operating analysis. This tells CAESAR II how much that location wants to move vertically (y) under the operating loads. So this becomes the “theoretical” hanger movement. Now, the “theoretical” cold load is calculated as Cold Load (CL) = HL + ky.
• CAESAR II adds the CL as a force and the spring stiffness as a restraint stiffness to all load cases of the model and then runs all the normal load cases.

In this article, We will design a variable spring hanger support by following the above Caesar II Algorithm. The steps for manual spring hanger design are explained below with an example.

Manual Spring Hanger Design Procedure

The example problem is shown in Fig. 1.

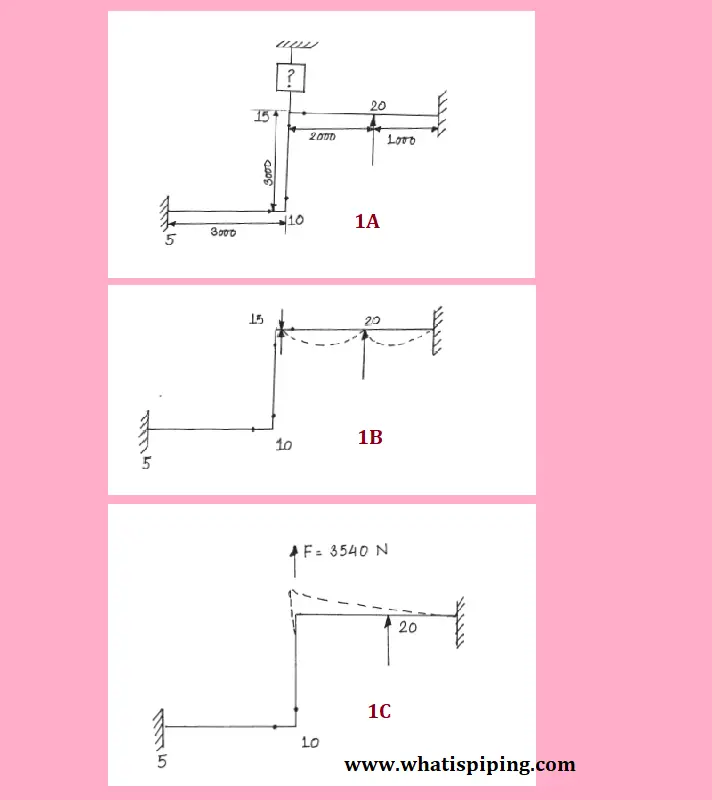
Let’s assume that we will design a variable spring hanger support at node 15 as shown in Fig. 1A. At node 20, the pipe is Resting.

To design the spring support, A weight run is to be taken with a Rigid double-acting Y restraint at node 15 (without friction). Assume the load computed to be 3540 N.

Now apply that force (3450 N) at node 15 in an upward direction and run an operating case. Note the lift-off at 20 as shown in Fig. 1C. Observe the travel at 15 let us assume it here as 5.785 mm.

In case, there is no lift-off in the nearby supports (Node 20) then the above-computed values will be the final Hot Load and Spring Travel.

But as the support at node 20 is lifted off, Remove the support at node 20 and Run a weight case with a rigid double-acting Y restraint at node 15 (without friction). Refer to Fig 2A. Assume, the load experienced at node 15 is now 3651 N.

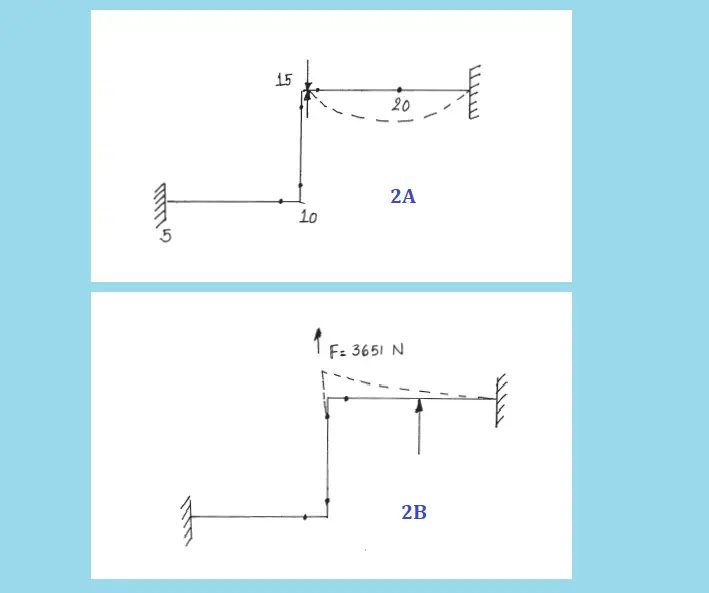
Now, an operating case runs are to be taken with 3651 concentrated loads (Fig. 2B) in an upward direction at 15. Suppose this time the travel is 5.829 mm.

Hence, for the above system
Computed Hot load = 3651 N.
Computed theoretical travel from cold to hot =5.829 mm.

On the basis of the computed hot load and the thermal travel one can estimate the maximum permissible spring rate as depicted below:

 k_max =(V_ar X HL)/ |y_th |——————– (a)

Where V_ar is the maximum permissible variation.

Now the computed hot load can be located in the columns of the spring support catalog table from the vendor. For that spring size select the spring series with a spring rate less than or equal to that calculated by (a).

The cold load can be calculated by

Cold Load= H.L + ky

The cold load calculated above is then located in the table under the same spring size.
If the cold load does not fall under the column of the selected size then a different spring series or spring of an adjacent size is to be selected.

Note that when specifying hanger’s hot and cold loads, It is important to add the anticipated hardware weights to these values especially if it is significant like trapeze assembly or large clamps, etc. The prime requirement being the necessity of the hanger to support hardware as well in order to avoid imbalance in the system by the weight of hardware.

Few more spring support related articles for you.

Spring Hanger Pipe Support Selection Procedure for Piping Stress Analysis
Technical and General requirements for Spring Hangers while purchasing.
TBE of vendor Spring hangers: Main points to consider before placing an order
Spring hangers: Common Interview Questions with Answers
Spring hanger selection and design guidelines for a Piping engineer using Caesar II
Basics of Pipe Stress Analysis