Maximum Shear Stress Theory: Tresca Theory of Failure

Maximum shear stress theory provides failure criteria for mechanical components made of ductile material. This failure criterion is developed by the French mechanical engineer, Henri Tresca, and based on his name maximum shear stress theory is also known as the Tresca theory of failure. Due to their enormous contribution to the field of plasticity, Henry Tresca is popular as the father of the field of plasticity.

Maximum shear stress theory is one of the two main failure criteria that are widely used in recent times for predicting the failure of ductile materials. To establish the failure criteria of material, all failure theories compare a specific parameter with the same parameter for the uniaxial tension test. The maximum shear stress theory is no exception and the parameter for comparison in Tresca theory is maximum shear stress.

“The maximum shear stress theory states that the failure or yielding of a ductile material will occur when the maximum shear stress of the material equals or exceeds the shear stress value at yield point in the uniaxial tensile test.”

Maximum shear stress theory formula

Let’s deduce the mathematical form of the above-mentioned Tresca theory statement.
Considering principal stresses, at the yield point, the principal stresses in a uni-axial test, σ₁ =σ_y; σ₂ = 0 and σ₃ = 0.
So the maximum shear stress at yielding: σ_sy =σ₁/2. Therefore σ_sy = σ_y/2

Now assuming σ₁ >σ₂ >σ₃; the maximum shear stress for the material is given by:

τ_max=(σ₁ -σ₃ )/2

Now comparing these to maximum shear stresses following Tresca theory, failure will happen when τ_max>=σ_sy

Safe Design Condition as per Tresca’s theory of failure

So the design of a mechanical component should be based on the following maximum shear stress theory equation

τ_max<=σ_sy or (σ₁ -σ₃)<=σ_y

The factor of safety (N) can also be calculated based on maximum shear stress theory and given by N=σ_sy /τ_max

Hence, the maximum permissible shear stress for designing a component as per maximum shear stress theory is given by τ_max =σ_sy /N

The failure envelope for Tresca’s theory of failure is provided in Fig. 1 below:

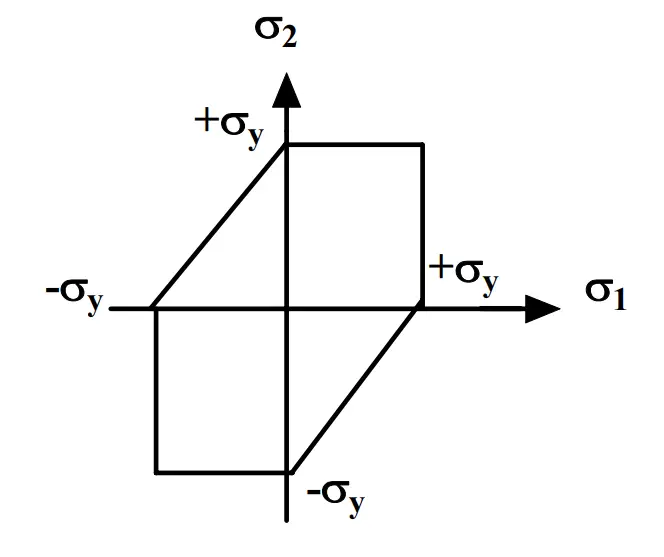
Steps for using the Maximum Shear Stress Theory

To use the maximum shear stress theory in problem-solving the following steps are necessary to be followed:

• Step 1: Determine the three principal stresses (σ₁,σ₂, and σ₃) from the tri-axial stress system using principal stress equations or Mohr’s circle method.
• Step 2: Find out the maximum (σ₁) and the minimum (σ₃) principal stresses.
• Step 3: Determine the value of the maximum shear stress τmax=(σ₁ -σ₃ )/2.
• Step 4: Find out the allowable stress value of the material; allowable stress= σsy /N or σy /2N as mentioned above (N=Factor of safety)
• Step 5: Compare the value calculated in step 3 with the allowable value found in step 4. If the Value at step 3 is less than the allowable value at step 4, then the design is safe as per the maximum shear stress theory.

Maximum Shear Stress Theory vs Von Mises Stress Theory

Von Mises and Tresca’s failure criteria are normally presented jointly with little discrimination between them. However, there are some differences between them which are tabulated below:

Maximum Shear Stress Theory	Von Mises Stress Theory
Maximum Shear Stress theory or Tresca theory of failure relates to the maximum shear stress of ductile materials.	Von Mises’s stress theory represents the maximum distortion energy of a ductile material.
This theory is considered to be more conservative. The Tresca theory, generally provides higher safety margins in certain applications.	Considered less conservative when compared with Tresca’s theory. It provides a more refined approach to determine yielding under complex loads.
Component cost designed based on Tresca theory increases.	Component Cost is Optimized for the design based on Von mises theory.
Required only two principal stress equations (σmax and σmin) to calculate the maximum shear stress.	Use all three principal stresses (σ1 ,σ2 , and σ3) in its equation for calculating Von Mises Stress.
Predicts yielding based on maximum shear stress differences.	Predicts yielding based on a combination of all principal stresses.

The following article describes the applicability of Tresca and Von-Mises Theory with respect to Piping and Pressure Vessel Applications: Tresca or Von Mises: Their Applicability in Piping and Pressure Vessel Applications.

The failure envelope for Tresca theory and Von Mises theory is given in Fig. 2:

Limitations of Maximum Shear Stress Theory

While the Maximum Shear Stress Theory provides a valuable framework for predicting material failure, it has its limitations. Some of the key limitations include:

1. Material Behavior: The theory is primarily applicable to ductile materials. For brittle materials, other criteria, such as the Mohr-Coulomb criterion, may be more appropriate.
2. Complex Loading Conditions: In cases where multi-axial loading is present, the Maximum Shear Stress Theory may not fully capture the material behavior.
3. Non-Isotropic Materials: The theory assumes isotropic material properties, meaning it may not apply to materials with directional dependence in their properties.
4. Temperature Effects: The theory does not account for changes in material properties due to temperature variations, which can significantly affect yield strength.
5. The maximum shear stress theory does not give accurate results for the state of pure shear stresses developed by the Torsion test.
6. The Tresca theory provides conservative results leading to an increase in component cost.

Applications of Maximum Shear Stress Theory

Structural Engineering

In structural engineering, the Maximum Shear Stress Theory is often applied to predict the failure of beams, columns, and other structural elements subjected to various loading conditions. By analyzing the shear stresses in components, engineers can ensure that structures remain safe under expected loads.

Mechanical Design

Mechanical components such as gears, shafts, and fittings often experience complex stress states. Using the Maximum Shear Stress Theory allows designers to assess the likelihood of failure in these components, leading to safer and more reliable designs.

Geotechnical Engineering

In geotechnical applications, the Maximum Shear Stress Theory can be used to analyze soil stability under various loading conditions. Understanding the shear strength of soil is crucial for designing foundations, retaining walls, and other earth structures.

Piping Engineering

In piping stress analysis, the Tresca theory is widely used.

In conclusion, the Maximum Shear Stress Theory remains a cornerstone of material failure analysis in engineering. Its ability to predict yielding under complex stress states is invaluable across various fields, from structural to mechanical engineering. Despite its limitations, it serves as a reliable criterion for assessing material behavior and designing safe structures and components.