What is Von Mises Theory of Failure? Formula for Von Mises Stress

Von Mises Stress criterion is one of the widely used criteria for designing ductile material engineering components. To judge if a design is within design limits and will work safely for its design life, Von Mises Stress Criteria prove to be highly effective. Von Mises’s stress concept is developed from the distortion energy theory and a highly preferred failure theory used in the mechanical design industry.

This theory is devised by James Clerk Maxwell in 1865, but in 1913 it was rigorously developed by Richard Edler Von Mises, an Austrian Jewish scientist and mathematician. Accordingly, the theory is popular as Von Mises’s Stress theory. In this article, we will explore more details about Von Mises’s Stress.

What is Von Mises Stress?

Von Mises stress is an equivalent stress value based on distortion energy to decide if a ductile material will fail (yield or fracture) under a given loading condition. The Von Mises failure theory indicates that A material will fail if the Von Mises stress or effective stress of that material under load is equal to or greater than the yield limit of the same material under a simple uniaxial tension test.

Equation/ Formula for Von Mises Stress

Failure of any material is decided by a simple tension test. In this test when the material reaches the yield point, the material is considered as failed. Now failure by distortion energy or Von Mises Stress theory compares two kinds of distortion energy.

• Case A: Distorsion energy for the actual case with complex loading conditions.
• Case B: Distorsion energy for the same material in the simple tensile test during failure.

As per Von Mises’s Stress theory, Failure will occur if Case A>=Case B. Mathematically, this can be explained as below:

Distorsion Energy (u_d) for the actual stress condition in terms of principal stress values (σ₁, σ₂, σ₃)

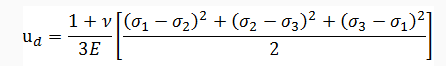
Again, the distortion energy for the uniaxial tension case at the time of failure is given as:

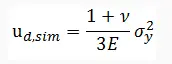
So, as per distortion energy theory,

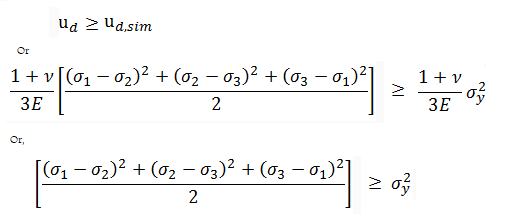
Now, the formula for Von Mises Stress, σ_v is given by

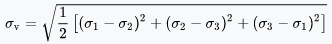
So, the above equation becomes, σ_v²>=σ_y²

So, the Von Mises failure condition can be simplified as follows:

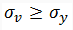
In the cases of plane stress, σ₃ = 0. The von Mises criterion reduces to,

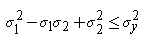
The failure envelope based on distortion energy or Von Mises Stress theory can be represented in two dimensions as follows:

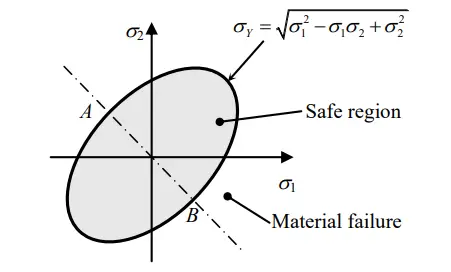
Steps for solving problems using the Von Mises Stress Theory

To use the Von Mises Stress theory in solving problems the following steps are required to be followed:

• Step 1: Calculate the three principal stresses (σ₁,σ₂, and σ₃) using principal stress equations or Mohr’s circle method.
• Step 2: Find out the Von Mises Stress (σ_v) following the equations mentioned above.
• Step 3: Determine the value of the allowable stress (σ_y/N) of the material. σ_y is the Yield Strength and N is the factor of safety.
• Step 4: Compare the value calculated in step 2 with the allowable value found in step 3. If the Value at step 2 is less than the allowable value calculated at step 3, then the design is safe as per the Von Mises stress theory.

Applications of Von Mises Stress Theory

During the mechanical design of elements, It is the duty of every engineer to keep the Von Mises Stress (σ_v) value below the yield strength (σ_y) of that material to make the design safe. This theory finds wide application in Finite Element Analysis.

In piping stress analysis and structural beam design, Von Mises Stress theory is applied to make the piping or structural beams safe from various loading conditions.

Difference between Von Mises’s theory and Maximum Shear Stress Theory

As distortion is always associated with shear stress; there are some similarities between both failure theories. The main differences between the Von Mises theory and the maximum shear stress theory are listed below:

• The Von Mises theory predicts ductile yielding with more accuracy as compared to the maximum shear stress theory. It is more real and less conservative than the maximum shear stress theory and hence, product cost reduces.
• Von-Mises theory uses all three principal stresses (σ₁,σ₂, and σ₃) in its equation, while the maximum shear stress theory uses only two (σ_max and σ_min ).

The following article describes the applicability of Tresca and Von-Mises Theory with respect to Piping and Pressure Vessel Applications: Tresca or Von Mises: Their Applicability in Piping and Pressure Vessel Applications