Young’s Modulus | Modulus of Elasticity | Elastic Modulus | Young’s Modulus of Steels

Young’s modulus, also known as the modulus of elasticity or elasticity modulus is named after the British physicist Thomas Young. This is a very useful parameter in material science. Young’s modulus specifies the measure of the ability of a material to withstand length changes under tensile or compressive forces. Young’s modulus is defined mathematically as the ratio of the longitudinal stress to the strain within the elastic range of the material.

Young’s Modulus Formula

As explained in the article “Introduction to Stress-Strain Curve“; the modulus of elasticity is the slope of the straight part of the curve. Young’s modulus is a fundamental mechanical property of a solid material that quantifies the relationship between tensile (or compressive) stress and axial strain. It is denoted by the letter “E” and mathematically expressed as E=Stress/Strain

E=σ/ϵ;

Here σ=Stress=Force (F)/Cross-Sectional Area (A)=F/A
ϵ=Strain=Change in Length(δl)/Original Length (l)=δl/l

So, E=(F/A)/(δl/l)=F*l/A*δl

As the strain is the ratio of two lengths, it is dimensionless.
Hence, the unit of Young’s modulus, E =the unit of stress=N/m² in the Metric system and psi (pound per square inch) in the English System.

For a specific material, the value of Young’s modulus or the modulus of elasticity is constant at a specified temperature. But with a change in temperature the value of Young’s modulus changes. With an increase in the material temperature, the modulus of elasticity of a material decreases.

The Youngs modulus does not depend on the geometry of the material. With the change in shape, length, the moment of inertia, weight, etc. the value of the modulus of elasticity does not change.

Which is more elastic: Rubber or Steel?

Young’s modulus signifies the elasticity of a material. The more the value of elastic modulus means the more elastic the material is. For example, as compared to rubber, the value of young’s modulus is more for steel material (Refer to Table 2). So, Steel material will regain its shape more easily as compared to the rubber on the application of force. Hence, Steel is more elastic than rubber. But sometimes it creates confusion when asked all of a sudden.

Use of Young’s Modulus

Young’s modulus is used

• To calculate the change in length (deformation or deflection) of a material under tensile or compressive loads.
• To calculate the amount of force required for a specific extension under specified stress.
• Young’s modulus can be used to calculate various other moduli (for example rigidity modulus, bulk modulus, etc) of a material.

Practical Applications of Young’s Modulus

There are numerous practical examples of Young’s modulus. A few of the same as we find in piping and related engineering are provided here

• The thermal stress generated in a piping system is calculated using Young’s modulus (E). Thermal Stress= Thermal Strain X E= E.α.ΔT; Here, α=co-efficient of thermal expansion and ΔT=change in length due to temperature.
• In flange leakage analysis using the ASME Sec VIII method, Young’s modulus is required to calculate flange stresses. Flange modulus of elasticity data is provided as input for design and ambient temperature conditions.
• For designing the load-carrying capability of steel and concrete structures, civil engineers use Young’s modulus along with allowable deflection data.

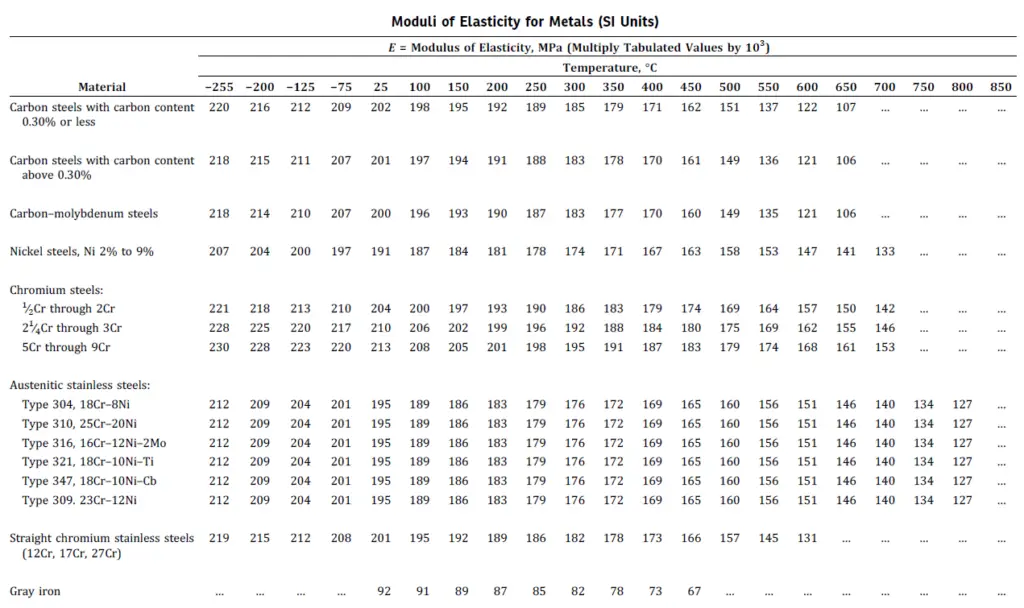
Young’s modulus of Steel

As steel is the most widely used material in industries, we will have a look at Young’s modulus of Steel for getting a rough estimate of the values. The following table provides typical values of Young’s modulus with respect to increasing temperature for ferrous materials.

Approximate Young’s Modulus for Some Other Materials

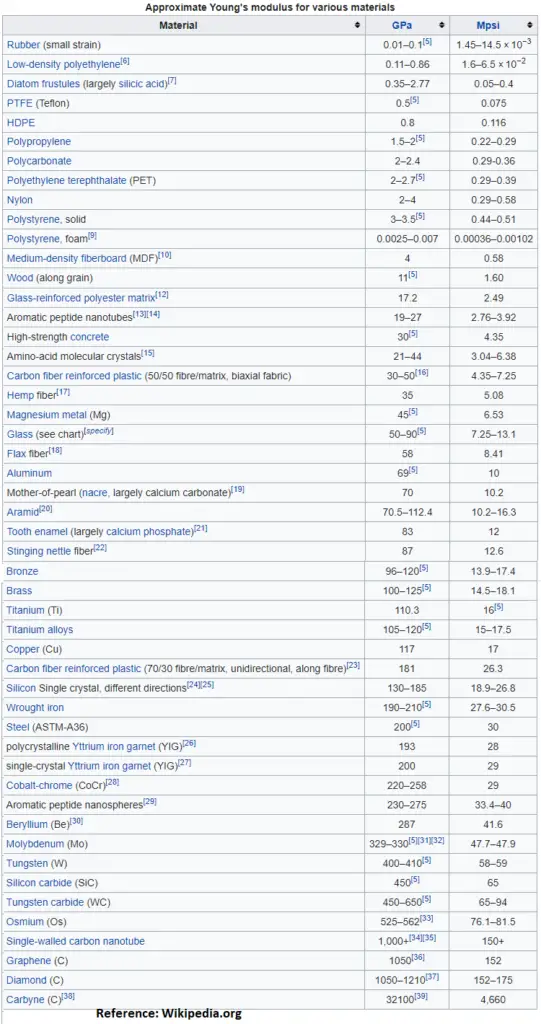
Table 2 below provides approximate Young’s modulus for some other well-known materials.

Factors Affecting Young’s Modulus

The main parameters that affect Young’s modulus of material are:

• Temperature (With an increase in temperature, Young’s modulus decreases)
• Presence of Impurity in the material like secondary phase particles, non-metallic inclusions, alloying elements, etc.