Bernoulli’s Equation & Principle: Definition, Derivation, Examples, Application

What is Bernoulli’s Principle?

Bernoulli’s principle provides a relationship between the pressure of a flowing fluid to its elevation and its speed. The conservation of kinetic, potential, and flow energies of a fluid stream and their conversion to each other is dictated by the Bernoulli principle. This principle is widely used in the study of the flow of water, air, or any other fluids having low viscosity. Many real-life engineering problems related to fluid flow can be easily solved by applying Bernoulli’s principle. This is the reason that Bernoulli’s principle is quite popular and studied in engineering and physics. This principle is deduced by Daniel Bernoulli and as per his name, it is widely known as Bernoulli’s principle.

Bernoulli’s Equation

Bernoulli’s equation provides the mathematical basis of Bernoulli’s Principle. It states that the total energy (total head) of fluid along a streamline always remains constant. The total energy is represented by the pressure head, velocity head, and elevation head.

The pressure head signifies the height of a column of fluid and is represented by P/ρg; the Velocity head signifies the kinetic energy and is represented by V2/2g, and the Elevation head signifies the potential energy and is represented by z. So, As per Bernoulli’s equation

(P/ρg)+(V²/2g)+z=Constant

The equation explains that, if an increase in the speed of a fluid occurs, there will be a decrease in static pressure or a decrease in the fluid’s potential energy. For flow inside horizontal pipes, where elevation head z is constant; the velocity increase will cause a decrease in pressure.

Assumptions in Bernoulli’s Equation

The following assumptions are made for deriving the above-mentioned Bernoulli’s equation:

• The fluid is ideal and it does not have any viscosity.
• Net frictional forces are negligible.
• The fluid is moving or flowing through a pipe or channel.
• The flow is incompressible and steady.
• The is no rotation in the flow.
• There is no heat transfer in the streamline.

Derivation of Bernoulli’s Equation

Refer to the image shown below that indicates the motion of a fluid particle of length ds in the s direction.

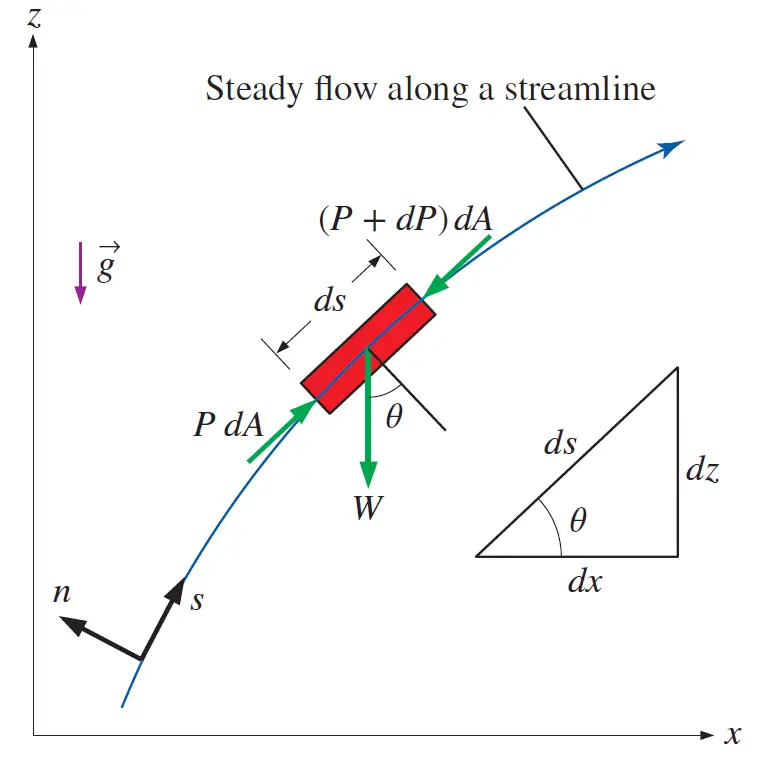
Applying Newton’s second law in that moving fluid particles in a steady flow we get,

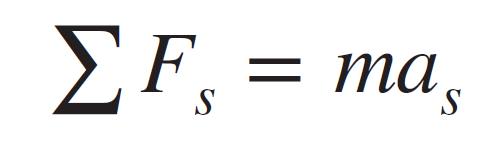
Now considering the assumptions mentioned above, the significant forces that will be acting in the s-direction are the pressure and the component of the weight of the particle in the s-direction.

Therefore, we can write the above equation as:

P dA − (P + dP) dA − W sin 𝜃 = mV (dV/ds );

where 𝜃 is the angle between the normal of the streamline and the vertical z-axis at that point, m = 𝜌V = 𝜌 dA ds is the mass, W = mg = 𝜌g dA ds is the weight of the fluid particle, and sin 𝜃 = dz/ds. Substituting we get,

−dP dA − ρg dA ds (dz/ds) = ρ dA ds V (dV/ds)

After simplification, we get

−dP − ρg dz = ρV dV

Now, V dV = 1/2 d(V²) and dividing each term by 𝜌 gives

dP/ρ + 1/2 d(V²) + g dz = 0

Integrating we get,

P/ρ +V2/2 + gz = constant

Dividing by g we get,

(P/ρg)+(V²/2g)+z=Constant

This is the famous Bernoulli equation, widely used in fluid mechanics for steady, incompressible flow along a streamline in inviscid regions of the flow.

Applications of Bernoulli’s Equation

The Bernoulli equation and principle find a wide range of applications in engineering fluid dynamics. This theory is applied to designing aerospace wings and for designing pipes for hydroelectric plants. Bernoulli’s equation is popularly used to:

• find pressures
• estimate flow through a pipe or nozzle
• find the velocity of the flow
• analyze fluid flow

Examples of Bernoulli’s Principle

The following examples of Bernoulli’s principle are widely popular.

Bernoulli’s Equation for Pump Sizing:

The volute in the centrifugal pump casing converts the velocity of the fluid into pressure energy by increasing the flow area. Here the conversion of kinetic energy into pressure energy is according to Bernoulli’s equation.

The pump head requirement is also decided by applying Bernoulli’s equation.

Design of Ejectors:

The conversion of the pressure energy of the motive fluid into the kinetic energy inside an ejector follows the principles of Bernoulli’s equation.

Design of Venturi Meters:

Venturimeters, widely used for flow measurement in the chemical, petrochemical, water, oil & gas industries are developed based on Bernoulli’s equation. Click here to know more details about venturimeters.

Bernoulli’s equation for designing Pitot Tube:

Pressure measuring instrument, Pitot Tube also works following Bernoulli’s principle.

Bernoulli’s equation to design the Automobile Carburetor:

Automobile Carburetors are a good example of Bernoulli’s equation. Bernoulli’s principle is used to meter the airflow inside the carburetor. The faster the air flows, the lower the static pressure, and the higher the dynamic pressure that decides the fuel intake into the airstream.

Working of Siphons:

Widely used Siphons also follow Bernoulli’s equation to evacuate or remove fluids from a container.

Application in Hydro-power Generation:

Hydroelectric engineers decide the water velocity from mountain reservoirs by knowing the elevation changes and using Bernoulli’s Principle.

Bernoulli’s Principle for Generating the Lift Force in Aeroplanes:

The top part of an airplane wing is curved while the bottom part is designed as a flat surface. This results in lower pressure on the top of the wing as compared to the bottom of the wing. This generated pressure difference (according to Bernoulli’s principle) creates the lift force for the plane.

Birds also fly in the sky using the same Bernoulli’s Principle.