What is Radiographic Testing? It’s Types, Principles, Procedures, Standards, Advantages, and Disadvantages

Written by Anup Kumar Dey in Engineering Materials,Mechanical,Pipeline,Piping Design Basics,Piping Interface

Radiographic testing (RT) is a non-destructive testing (NDT) method widely used to assess the integrity of materials and structures without causing damage. This technique plays a critical role in industries such as welding, aerospace, automotive, manufacturing, pipelines, and construction, ensuring safety and quality through precise evaluations. In this article, we’ll explore the principles, types, advantages, applications, and safety considerations of radiographic testing.

1. What is the Radiographic Testing?

Radiographic testing, or radiographic examination, is a non-destructive testing (NDT) method for examining the internal structure of any component to identify its integrity. Radiographic Testing or RT uses x-rays and gamma-rays to produce a radiograph of the test specimen that shows changes in thickness, defects or flaws, and assembly details to ensure optimum quality. Radiographic testing of welds to ensure weld quality is a widely used industry practice. Radiographic testing in welding is a highly dependable way to detect weld defects like cracks, porosity, inclusions, voids, lack of fusion, etc. in weld interiors. Because of its high dependability, radiographic testing is widely used in the oil & gas, aerospace, transport, military, automotive, manufacturing, offshore, petrochemical, marine, and power generation industries.

2. Radiographic Testing Principle

In Radiography Testing, the part to be tested is placed between the radiation source and a piece of sensitive film or detector. Once the x-ray or gamma-ray radiation is started, the test part will hinder some of the radiation by its material density and thickness. Thicker and denser material will allow less radiation to pass through the specimen. The film (or an electronic device) records the amount of radiation (known as a radiograph) that reaches the film through the test specimen. By studying the radiograph data, defects can easily be recognized. If the material is sound without any defect, entire rays will evenly pass through the material. But for materials containing flaws, rays passing through the flaws will get absorbed to a small extent due to the change in density.

Defects in parent metal reduce its density and hence they transmit radiation much better than the sound metal. Hence the radiograph film appears to be darker in the area exposed by the defects.

The penetration power of rays is dependent on the energy of the radiation. Radiation with higher energy can penetrate thicker and denser materials. As high-energy x-rays and gamma-rays are highly radioactive, local rules must be strictly followed.

In radiographic testing, defects are detected using thickness variation. So, the larger the variation, the easier the defect is to detect. But when the path of rays is not parallel to a crack, the thickness variation is less, and thus the crack may not be visible. That’s why it is always suggested to perform radiographic testing by sending rays at various angles.

In industrial radiography, various imaging techniques are employed to display the final results. These include:

Film Radiography
Real-Time Radiography (RTR)
Computed Tomography (CT)
Digital Radiography (DR)
Computed Radiography (CR)

Each of these methods offers distinct advantages, catering to different inspection needs and preferences.

Industrial radiography utilizes two primary radioactive sources: X-rays and Gamma rays. Both types use high-energy, short-wavelength versions of electromagnetic waves, allowing for effective penetration of materials. Due to the inherent risks associated with radioactive materials, strict adherence to local safety regulations is crucial during operations.

Computed Tomography (CT) is one of the advanced non-destructive testing (NDT) methods offered by TWI for industrial applications. This technique generates both cross-sectional and 3D volume images of the inspected object.

CT provides a significant advantage over traditional 2D radiography by eliminating overlay, allowing for a clearer examination of the internal structure of components. This capability enables a thorough analysis of various parts, facilitating improved detection of internal features and flaws.

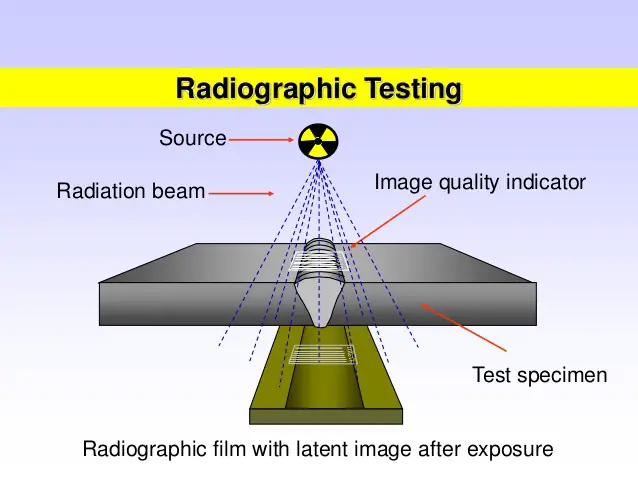
2.1 Types of Radiographic Sources

Radiographic testing utilizes various sources, including:

Conventional Sources
Micro-focus X-ray Equipment
Nano-focus X-ray Equipment
Linear Accelerators (Linac)
Betatrons
Synchrotrons
Isotropic Sources such as Iridium-192, Cobalt-60, Thulium-170, Ytterbium-169, Caesium-137, and Selenium-75.

2.2 Types of Radiographic Detectors

There are several types of radiographic detectors available, including:

Radiographic Films with grain sizes from D4 to D7
Radiographic Image Intensifiers
X-ray Sensitive Vidicons
Fluorescent Screens and Charged Coupled Devices (CCDs)
Imaging Plates
Digital Flat Panels, such as Amorphous Selenium Panels and Amorphous Silicon Panels
Linear Diode Arrays

2.3 Key Factors in Radiographic Imaging

A crucial aspect of radiographic imaging includes the contrast of the subject, film contrast, and image definition. These factors are influenced by several elements:

Energy Utilized in the Process
Wave Intensity
Scattered Radiation resulting from the interaction of beams with the specimen
Focal Spot Size
Characteristics of the Detector Used

3. Radiographic Testing Procedure

Depending on project requirements the radiographic testing procedure will vary a little. The following paragraphs provide sample procedural steps for radiographic testing.

Step 1- Surface Preparation: Surface irregularities must be removed so that they can not mask or confuse the image as a defect. The finished surface of all butt welded joints should be flushed with the base material.
Step 2- Selecting the right radiation source and radiographic film: Depending on radiographic sensitivity and material thickness radiation source (x-ray or gamma-ray) must be decided. Fine-grain high-definition radiographic films can be used.
Step 3- Selection of Penetrameter: As per SE 142 or SE 1025 (for whole type) and SE-747 (for wire type), ASME V & ASME Sec VIII Div I, whole type or wire type penetrameter need to be selected.
Step 4-Radiographic testing technique: Single or Double wall exposure technique is used. Source-to-object and object-to-source distances must be established beforehand.
Step 5- Defect inspection and removal: The radiograph is to be studied for probable defects and repaired if the defect is observed.
Step 6- Recording: All data need to be properly recorded.

4. Acceptance Criteria for Radiographic Testing

For process Piping: The acceptance criteria for radiographic testing shall be as per table 341.3.2 A of ASME B31.3 for normal fluid service, with the exception of piping class E.
For structural steel: The acceptance criteria for the non-tubular structure shall be in accordance with the requirement section 6.12.1 of AWS D1.1 and for tubular joints section 6.12.3 of AWS D1.1

5. Types of Radiography

Radiographic testing (RT) encompasses various techniques, including conventional and digital methods, each with its own advantages and limitations.

5.1 Conventional Radiography

Conventional radiography relies on sensitive film that reacts to emitted radiation, capturing an image of the tested part. This image can be analyzed for potential damage or flaws. However, a significant drawback is that each film can only be used once, and the processing and interpretation of the images can be time-consuming.

5.2 Digital Radiography

In contrast to conventional methods, digital radiography uses digital detectors to display radiographic images on a computer screen almost instantly. This technique significantly reduces exposure time, enabling quicker interpretation of results. Digital images are generally of higher quality, allowing for the identification of material flaws, foreign objects, weld repairs, and corrosion under insulation (CUI). Common digital radiography techniques in the oil and gas, as well as chemical processing industries, include computed radiography, direct radiography, real-time radiography, computed tomography, and automated radiographic testing.

5.3 Computed Radiography

Computed radiography (CR) employs a phosphor imaging plate instead of film. While quicker than conventional film radiography, it is slower than direct radiography. CR involves capturing an image on the phosphor plate and converting it into a digital signal for visualization on a computer. Although image quality is generally fair, it can be enhanced using various tools. However, caution is necessary to ensure that minor defects are not obscured by adjustments.

5.4 Direct Radiography

Direct radiography (DR) is similar to CR but uses a flat panel detector to capture images directly, which are then displayed on a computer screen. DR offers faster imaging and higher-quality results, but it comes with a higher cost compared to CR.

5.5 Real-Time Radiography

Real-time radiography (RTR) allows for instantaneous image viewing and analysis. This method emits radiation through an object, interacting with a phosphor screen or flat panel detector containing microelectronic sensors. The resulting digital image reflects varying radiation levels; brighter areas indicate thinner or less dense sections, while darker areas correspond to thicker components. RTR eliminates the need for physical storage, making it easier to archive and transfer images. However, it may exhibit lower contrast sensitivity, uneven illumination, and other issues that can affect image quality.

5.6 Computed Tomography

Computed tomography (CT) captures numerous 2D radiographic scans to create a detailed 3D image of the component. In industrial applications, CT can be performed in two ways: one involves rotating the radiation source and detector around a stationary component, ideal for larger parts, while the other method rotates the component itself, suitable for smaller or more complex geometries. Though CT requires significant time, expense, and data storage, it delivers highly accurate, repeatable images, minimizing the potential for human error.

5.7 Automated Radiographic Testing

Automated radiographic testing (ART) was designed for faster, safer, and more consistent detection of CUI and internal corrosion in above-ground piping and pipelines. ART utilizes a semi-autonomous motion control platform that carries low-level X-ray emitters, projecting onto CMOS and photon detectors that produce radiographic maps in seconds. This technology enables robotic services to efficiently radiographically map large areas without disrupting service or removing insulation, providing immediate digital images for on-site evaluation.

6. Codes and Standards for Radiographic Testing

Widely used codes and standards for radiographic testing are:

ISO 5579, Non-destructive testing – Radiographic examination of metallic materials by X- and gamma-rays – Basic rules
ASME SE: Standard Method for Controlling Quality of Radiographic Testing.
ASME SE 94: Recommended Practice for Radiographic Testing
ASTM E 801, Standard Practice for Controlling Quality of Radiological Examination of Electronic Devices
API 1104, Welding of Pipelines and Related Facilities: 11.1 Radiographic Test Methods
AASME SE V: Boiler and Pressure Vessel – Non-Destructive Testing.
ASTM 1161, Standard Practice for Radiologic Examination of Semiconductors and Electronic Components
ISO 10675-1, Non-destructive testing of welds – Acceptance levels for radiographic testing – Part 1: Steel, nickel, titanium, and their alloys
SNT-TC-1A: Recommended Practice for Personnel Qualification and Certification in Non-destructive Testing.
ASTM E 592, Standard Guide to Obtainable ASTM Equivalent Penetrameter Sensitivity for Radiography of Steel Plates
ASTM E 1030, Standard Test Method for Radiographic Examination of Metallic Castings
ASTM E 1815, Standard Test Method for Classification of Film Systems for Industrial Radiography
EN 12681, Founding – Radiographic examination
ASTM E 1032, Standard Test Method for Radiographic Examination of Weldments
ISO 4993, Steel and iron castings – Radiographic inspection

7. Advantages of Radiographic Testing

Radiographic testing (RT) offers numerous advantages over other non-destructive testing (NDT) methods, particularly in its ability to assess internal structures and complex geometries. Some of the key advantages of radiographic testing are

Assembled components can easily be inspected.
The surface preparation requirement is minimal.
RT is known for its exceptional accuracy, capable of detecting even minute flaws that might go unnoticed with other techniques. Both surface and subsurface flaws can be detected.
Easily verify internal defects on complex items/structures
Automatically detect and measure internal flaws
Dimensions and angles of the sample can be measured without sectioning.
Radiographic testing is one of the best NDT methods in lieu of golden joints.
RT can be applied to a wide range of materials, making it suitable for various applications across different industries.
The results from radiographic testing are visually represented and can be permanently documented, either digitally or on film. This eliminates concerns about data loss and simplifies analysis.
X-rays and gamma rays have excellent penetration abilities, allowing them to reveal detailed internal structures within the test material.
Unlike some NDT methods that may misinterpret surface anomalies, RT can accurately identify internal defects, providing clear insights into their nature, size, and depth. This simplifies the process of detecting fabrication errors.

8. Disadvantages of Radiographic Testing

The main disadvantages of radiographic testing are

Highly hazardous, so proper care must be exercised.
The high degree of skills and experience required.
Costly affair; the specialized equipment required for RT, designed to use penetrating radiation, can be expensive to acquire and maintain.
Slow process.
Two-sided access to components is required.
Interpreting the depth of detected defects can be challenging, as radiographic results may not provide clear information on the depth of indications.

9. Applications of Radiographic Testing

Industrial radiography is mostly used for inspection purposes. The industries that make frequent use of RT are

Weld Inspection: Commonly used to evaluate weld quality and detect defects in pipelines, pressure vessels, and structural components.
Casting Inspection: Ensures the integrity of cast components by identifying internal voids or inclusions.
Aerospace Components: Critical in the aerospace industry for inspecting aircraft parts and ensuring safety standards.
Automotive Industry: Used to inspect components for structural integrity and safety, such as engine parts and chassis.
Nuclear Industry: Plays a vital role in ensuring the safety and integrity of nuclear reactor components.
Military Defense: Critical for evaluating the integrity of military equipment and munitions, ensuring they meet high safety and performance standards.
Offshore Industries: Essential for inspecting pipelines, risers, and structural components in challenging marine environments, helping to prevent leaks and failures.
Marine Industry: Used to assess the condition of ship hulls, propellers, and other critical parts, ensuring the safety and reliability of maritime operations.
Power Generation Industry: Employed to inspect components in power plants, including boilers and turbines, to maintain operational efficiency and safety.
Petrochemical Industry: Vital for examining pipelines, vessels, and storage tanks to prevent leaks and failures in the transportation and processing of hazardous materials.
Waste Management: Used to inspect waste containers and processing equipment, ensuring compliance with safety regulations and preventing contamination.
Manufacturing Industry: Widely applied to inspect castings, welds, and assembled parts, helping to maintain quality control throughout the production process.
Transport Industry: Utilized to ensure the safety and reliability of transport components, including railways and road infrastructure, by detecting potential flaws.
Medicine Industry: Radiographic testing plays a critical role in the medical industry, contributing to both diagnostics and treatment.

Radiographic testing is a powerful non-destructive technique that plays a critical role in ensuring the safety and reliability of materials across various industries. Its ability to detect internal defects without damaging components makes it indispensable for quality assurance and regulatory compliance.

Further Studies on radiographic testing

Radiographic Testing.pdf (hu.edu.jo)

Design of Centrifugal Compressor Piping and Appurtenances excluding Anti-Surge Systems

Written by Ankur Srivastava in Mechanical,Pipeline,Piping Design Basics,Piping Interface,Process

Centrifugal compressors are widely used in process plants to compress gases. Centrifugal Compressors, being rotary equipment, are highly sensitive and prone to vibration. So, the connected piping system must be designed with care to get optimum performance. In this article, we will explore the design of centrifugal compressor piping and appurtenances.

Refer to Fig. 1 below which shows a typical process flow diagram of a single-stage centrifugal compressor.

The surge control or anti-surge system shown in the above PFD is a very basic representation of the system. There are many variations to the basic representation shown in the PFD including the measurement of temperature at suction and discharge providing feedback to the anti-surge system.

The design considerations for the centrifugal piping are divided into two parts.

Suction Piping Design Considerations and
Discharge Piping Design Considerations

Centrifugal Compressor Suction Piping Design

Process Considerations for Suction Piping Design

The rule of thumb is to size the suction piping of the compressor’s first stage such that the pressure drop should not exceed 3.4 kPa or 1% of operating pressure (whichever is smaller), and a maximum actual velocity of 9.1 m/sec. To determine the velocity, use the formula provided in Eqn. 1, and to determine the pipe’s internal diameter based on the maximum velocity rule of thumb use the formula provided in Eqn. 2 of Fig. 2 below.

**Fig. 2: Formula for Centrifugal Compressor Suction Pipe Diameter Calculation**

Where

V_gact = actual gas velocity, m/s
T = gas temperature at suction, K
d = Pipe ID, mm
P = Pressure, kPa (abs)
Q_g = gas flow rate, Sm³/h (Note: Sm³/h flow rate is at 15⁰C and 101.325 kPa(abs))
Z = gas compressibility factor at T, P

Piping Considerations for Suction Piping Design

1. Straight Length Requirement

The following figures (Fig. 3 & Fig. 4) establish the practice for straight length ahead of the inlet or suction nozzle of the compressor. The sketch is applicable for multistage compressors including the inlet or suction piping of the subsequent stage after the first stage. The sketch is for the base case for the suction piping provided with one long radius elbow (plane parallel to the rotor). For cases other than the base case various multipliers are used to define the straight length of pipe required ahead of the suction nozzle. All the other cases are also discussed as a subset of the base case using the multipliers:

**Fig. 3: Compressor Inlet Correction Factors for various Piping Arrangements**

**Fig. 4: Various Piping Configurations for Compressor Suction**

When suction piping straight length for axial or single-stage compressors needs to be found, the straight length obtained based on the above figures for the various piping arrangement cases shall be multiplied by an additional factor of 1.25.

2. Slope of Compressor Suction Piping

Piping shall slope continuously downward from the suction scrubber to the compressor suction connection. A desirable configuration for the slope of the suction piping would be to provide a slope from the upstream flange of the suction line isolation valve towards the suction scrubber and a slope towards the compressor suction nozzle from the downstream of the suction line valve. Valves shall be located only in horizontal piping.

3. Suction Strainer

The provision of suction strainers is mandated in most applications to trap any solid particles that can cause damage to the compressor internals. Screens and Filters used shall have high mechanical integrity and strength to prevent their failure and entry into the compressor casing. All strainers shall be installed as close to the compressor as feasible.

When temporary suction strainers are used, pressure gauge taps shall be provided upstream and downstream for the commissioning of the compressor. When the temporary strainers are removed, the tapped connections shall be plugged, and seal welded.

4. Low Point Drain

Compressors having a suction nozzle orientation such that the suction line connects from the bottom forming a low point in the suction line shall be provided with a small boot or sump with a local gauge glass and a local drain connection to drain any condensed liquid. The boot or sump shall be provided as close as feasible to the compressor suction nozzle and at the lowest point in the suction piping.

5. Lube & Seal Oil System

Hose connections shall not be used in lube and seal oil systems of compressors.

Centrifugal Compressor Discharge Piping Design

Process Considerations for Discharge Piping Design

The interstage and discharge piping thumb rule for sizing is a pressure drop not to exceed 2 percent of operating pressure or 34 kPa (whichever is higher) and a maximum actual velocity (adjusted for temperature and compressibility) of 15.2 m/sec.

Equations 1 & 2 (Fig. 2 above) can be used for evaluating the velocity for a given diameter and the discharge pipe diameter based on the aforementioned maximum velocity.

Maximum velocity considerations are also based on noise criteria observed in gas lines.

Many operators of natural gas transmission pipelines have concluded that velocities up to 20 m/s are acceptable with due consideration of noise. Companies like Shell recommend velocities of 5-10 m/s for continuous operation in long-distance natural gas pipelines and a maximum of 20 m/s for intermittent operation.

Fig. 5 below shows a typical centrifugal compressor piping system.

**Fig. 5: Typical Centrifugal Compressor Suction and Discharge Line**

Other Important Design Considerations for Centrifugal Compressor Piping System

Minimum Line Sizes & End Connections

Normally line sizes below 2” are avoided. Threaded connections are not used due to pressure and temperature considerations. For hydrocarbon and other flammable/toxic gases, threaded connections are strictly prohibited. Most designers prefer to use Schedule 80 pipes in high-pressure gas compression applications.

Suction Isolation Valve

For isolating the compressor suction a suction isolation valve is provided in the suction piping which is manually operated. The valve location shall be evaluated on a case-to-case basis. For large-size valves, the manual valve is provided with a gear operator for ease of operation.

Discharge Isolation Valve

For isolating the compressor discharge a discharge isolation valve is provided in the discharge piping which is manually operated. The valve location shall be evaluated on a case-to-case basis, with the general objective of locating it as close as possible to the discharge connection. For large-size valves, the manual valve is provided with a gear operator for ease of operation.

Discharge Check Valve

The check valve prevents reverse flow and reverses the rotation of the compressor unit which can cause serious damage to the seals and bearings. Install the check valve as close as possible to the discharge nozzle considering all aspects of accessibility and maintainability.

Blowdown Valve

The function of the blowdown valve is to relieve the high-pressure gas trapped in the compressor system during a breakdown or a planned shutdown. Most operators use automatic blowdown valves to reduce the hazards of trapped gas. If the blowdown valve has been tied into a closed vent system to route gas to a safe area for flare or vent, a second separate blowdown valve may be required. This valve should vent directly to the atmosphere, with nothing else tied into its line. This practice prevents backflow from the closed vent system while the compressor is down for maintenance and permits small leaks of gas from the compressor to vent safely. The Process Flow Diagram flowsheet shows a manual valve to accomplish this. Occasionally, a three-way valve is used for this purpose.

Flare Valve

As suction pressure increases, the head requirement will decrease, and the gas flow rate will increase. The increased flow rate beyond the design maximum may force the compressor to operate in the stonewall region, which would result in damage to the machine, or it may create too high a power demand for the driver. To avoid these possibilities, a flare valve tied to the vent header is installed at the suction side of the compressor. The valve is operated by a pressure controller, which is attached to the suction line upstream of the suction scrubber. The flare valve will also open if the compressor shuts down, allowing the operator time to react before the process must be shut in.

Suction Throttle Valve

Flaring or venting may be reduced by installing a control valve in the suction line (not shown in the PFD illustrated). This valve regulates either flow or pressure to avoid operating the compressor in the stonewall region or overloading the driver. As this valve begins to throttle flow into the compressor, pressure will begin to increase in the upstream equipment. If the high flow condition persists, the flare valve will eventually open. However, if the upstream equipment is rated for a high enough pressure and there is a large enough difference between the throttle valve and flare valve set pressures, it is possible that surges of gas can be processed without flaring.

Emergency Shutdown Valves (ESDV)

An ESDV is an actuated valve with generally a full close action designed to stop the flow of a hazardous fluid in the enclosed system or prevent loss of containment to the external environment, upon the detection of a dangerous event. The ESDV thus acts to mitigate any catastrophic damage to equipment and the environment. In many cases, an ESDV by its action can prevent injury or loss of life due to a catastrophic event or accident.

Quarter-turn valves are the most common ESD valves for actuation. They can be hydraulically, pneumatically, or electrically operated.

Centrifugal compressors in all sizes shall have a remote-operated emergency shutdown valve in the suction piping. The compressor suction isolation valve, if remotely operated, can also be the emergency shutdown valve. For field operation of the ESDV, a pushbutton station with a position indicator shall be located in the area of the compressor, at least 15m away, and in a location that is easily accessible. Location consideration shall also take into account that the pushbutton station is not exposed to fire. The remotely operated ESDV shall also be operable from the central control room.

Fireproofing of remote-control emergency shutdown valve assemblies is required. All resilient seated emergency shutdown valves shall be of a fire-safe design.

Silencers (as required)

Silencers are required to suppress the intake noise from compressors which is generated by the high-speed rotation of the impeller(s). They may be installed as per the application on a case-to-case basis. Silencers shall be located as close as possible to the suction and discharge nozzles as feasible. On the discharge side, the silencer is required to be located downstream of the check valve. To optimize the layout, the silencers may be arranged with side or end connections. Silencer shells and flanges shall conform to the piping class and specifications of the respective piping they are connected with.

Few more related articles for you.

Basics of Centrifugal Compressors: A presentation
A Brief Overview of Centrifugal Compressor System Process Design
Compressor Piping Layout: Compressor Piping Design
Stress Analysis of Centrifugal Compressor Connected Piping Systems using Caesar II
Difference between Centrifugal and Reciprocating Compressor

What is Time History Analysis? Steps with example

Written by Rajesh Ramadas in Caesar II,Piping Stress Analysis,Piping Stress Basics

Time history analysis is quite popular in pipe stress analysis as it provides the most realistic specification of dynamic loads in CAESAR II. The program’s modal time history analysis can simulate system response to several force-versus-time events. Time history is best suited to impulse loadings (slug, water hammer, PSV reaction, etc.) or other transient loadings where the profile is known. Only one dynamic load can be defined as a time history analysis. This dynamic load case can be used in as many static/dynamic combination load cases as necessary. The single load case may consist of multiple force profiles that can be applied to the system simultaneously or sequentially. Each force versus time profile is entered as a spectrum with an ordinate of Force (in current units) and a range of Time (in milliseconds). The profiles are defined by entering the time and force coordinates of the corner points defining the profile. In this article, we will explore the methods followed for dynamic time history analysis using Caesar II considering an example of a slug flow system.

Reason for Dynamic Time History Analysis

While the adoption of a pseudo-static approach, the application of a static load corrected using an appropriate dynamic load factor, can also provide a conservative result. In some short pipe routing it is required to check how the pipe routing responds to loads with very short durations. This is why time history analysis is often considered a better approach and can be performed with commercial software such as CAESAR II.

Time history analysis provides a method of assessing displacements, stress, and reactions developed in a piping system over time. In order to carry out such an analysis there is a need to be able to define the loading, be it the forces associated with a fluid slug traveling through a piping system.

Time History Analysis Example using Caesar II

In the following paragraphs, we will discuss the time history analysis for the design of a Flowline of a typical Wellhead piping system. The pipeline system shown in Fig. 1 is used for dynamic time history analysis.

**Fig. 1: 3D model of the system under Time History Analysis**

Time History Analysis Input

Time history analysis input can be divided into three steps listed below:

Modification in the Static Model
Dynamic Load Definition and
The setting of Dynamic Control Parameters

1. Modification in the Static Model

Element length needs to be kept at a minimum for getting proper mass distribution, mode shapes, and natural frequency of the system. The following thumb rule for maximum element length can be followed:

Minimum of 10 times of nominal diameter i.e 10D and 6000 mm.
5 times of nominal diameter near anchor or line stop supports.
at least 1 node in between two supports.
At least 1 node between two bends.

Support stiffness values can be considered to get more accurate results.

2. Defining Dynamic Loads for Time history analysis

The main inputs required to enter the spreadsheet for dynamic time-history analysis are listed below:

Slug Force can be calculated by collecting fluid density and velocity from the Process department.
The time duration for traveling from one elbow to another can be calculated by dividing the pipe length between two elbows by flow velocity. Two-time durations need to be calculated. Those are slug duration and slug periodicity. Both of these time durations will be required to create a time history spectrum for analysis. So, before opening the caesar ii dynamic input module, Calculate slug force, slug duration, and periodicity for each elbow node where the slug is expected to hit.

Let’s move on to the actual caesar ii time history analysis module. Before starting the dynamic module the static analysis need to be performed and the system must be safe in all static stress analysis aspects.

Step 1-Starting the Time history module: Open the Caesar II time history module as shown in Fig. 2

**Fig. 2: Starting time history module in Caesar II**

Step 2- Force Time profile definition: Refer to Fig. 3 below to understand the node numbers of the system.

**Fig. 3: Time history analysis model with node numbers**

Slug force needs to be applied in each elbow node (50, 60, 120, 130, 140, etc) as shown in the above system. For each elbow node, force-time profile is to be created for time history analysis. As shown in Fig. 4 enter values corresponding to each elbow node.

**Fig. 4: Force-Time Inputs for profile generation**

Input Range type as time, Ordinate Type as Force, Range Interpol, and Ordinate Interpol as Linear. Now click on the highlighted button (Fig. 5) for generating a time-history profile for each node entered in Fig. 4.

**Fig. 5: Time history spectrum generation**

Now select each node one by one and enter the earlier calculated time and force values to generate a spectrum for each node as shown in Fig. 6 below:

**Fig. 6: Creating Time History Spectrum**

Further steps of creating Force Sets, Time history load cases, and static-dynamic load combinations are the same as explained in the earlier article “Slug Flow Analysis Using Dynamic Spectrum Method in Caesar II“. Kindly click on the link provided to learn the same.

3. Setting up the Dynamic Control Parameters

The control parameters can be set as provided in Fig. 7

**Fig. 7: Control Parameters for Time History Analysis**

The Advanced control parameters can be set as provided in Fig. 8

**Fig. 8: Advanced Control Parameters for Time History Analysis**

Once the input parameters are entered and the control parameter is set up as explained above, run the analysis to get output results. The output results to be checked are similar to the earlier article titled “Slug Flow Analysis Using Dynamic Spectrum Method in Caesar II“

Response Spectrum vs Time History Analysis

The response spectrum method is a linear dynamic analysis method but Time history analysis is normally a non-linear analysis. Time history is a more detailed analysis involving the time instant.

In time history analyses the structural response is computed at a number of subsequent time instants. In other words, time histories of the structural response to a given input are obtained as a result. In response spectrum analyses the time evolution of response cannot be computed. Only the maximum response is estimated. No information is available also about the time when the maximum response occurs.

Factor of Safety: Definition, Equation, Examples, Calculator

Written by Anup Kumar Dey in Civil,Mechanical,Piping Design Basics,Piping Interface,Piping Stress Analysis,Piping Stress Basics

The factor of safety or safety factor is a very important term in engineering design. While designing any Engineering product or component, safety is of utmost importance. To ensure the safety of those items, each component is designed to bear more loads than its actual operating loads. So, there will always be some margin or cushion as compared to its operating capabilities. This is ensured during the design stage by considering a suitable factor of safety. In this article, we will discuss the following:

What is the Factor of Safety?
Importance of Factor of Safety in Engineering Design
Factors Affecting the Factor of Safety
Equation of Factor of Safety
Examples of Factors of Safety, and
Many More…

What is the Factor of Safety?

The factor of safety is defined as the ratio of the ultimate stress of the component material to the working stress. It denotes the additional strength of the component than the required strength. Factor of Safety is also popular by its abbreviated form FoS or FS. It is a numerical value that quantifies the safety level and reliability in engineering design. So, the factor of safety provides a buffer zone for engineers to ensure that their design will not fail under certain extreme conditions.

Importance of Factor of Safety

A factor of safety is related to the safety of people. It reduces the risk of failure of a component by adding some cushion in the design. Also, there always will be some hidden circumstances or unknown parameters that can not be considered accurate in design. At the same time, the reliability of the material is not 100% and the load used in design calculation is not the maximum load. So the factor of safety or safety factor provides protection against those unknown events to some extent.

Although all components are designed with a factor of safety, it’s always suggested to use those components within their design limit.

Factors Affecting Determination of Factor of safety

Component design codes & standards normally provide a minimum factor of safety for that component. However, choosing the exact safety factor is dependent on various parameters like

Material type Ductile vs. Brittle
Loading type Static vs. dynamic
Whether cyclical loads
The intensity of stress concentration
Unforeseen Misuse of the component
Accuracy and stress complexity during a calculation, Reliability of Data used in the factor of safety calculation.
Environment and design temperature and pressure.
Impact of failure
Cost of component or material
Corrosion rate
Maintenance frequency
Application of the component
Industry Standards and Regulations
Historical Data and Experience
Design Optimization
Client or Stakeholder Requirements

Factor of Safety Equation | Formula for Factor of Safety

As defined in the first paragraph, the factor of safety is a ratio of two loads or two stresses. Mathematically factor of safety can be expressed as

Factor of safety=Ultimate Load (Strength)/Allowable Load (Stress)

As understood from the above equation the allowable stress is always less than the ultimate failure stress. Hence, the factor of safety is always greater than 1. The ultimate stress for brittle material is considered as ultimate tensile strength and for ductile material is considered as yield strength.

Also, as the equation for the factor of safety is the ratio of two stress or load values, it is dimensionless. The difference between the Factor of Safety and 1 is known as the Margin of Safety. So,

The margin of safety = (Factor of safety-1).

Examples of Factors of Safety

Typical examples of the factor of safety for some materials depending on application and loading types are listed below in Table 1. However, please note that the table only provides a typical range or typical values to provide an example. Actual values for the factor of safety must be taken from the design standard of the relevant component. For example, the factor of safety for pressure vessel design must be taken from the ASME Sec VIII code.

Sr No	Member	Typical Factors of safety range
1	Structural Members in building services	2
2	Pressure Vessel	3.5 to 4
3	Automobiles	3
4	Aircraft and Spacecraft	1.2 to 3.0
5	Aircraft components	1.5 to 2.5
6	Boilers	3.5 to 6
7	Bolts	8.5
8	Cast-iron wheels	20
9	Engine components	6.0 to 8.0
10	Heavy duty shafting	10.0 to 12.0
11	Lifting equipment – hooks	8.0 to 9.0
12	Pressure vessels	3.5 – 6
13	Turbine components – static	6.0 to 8.0
14	Turbine components – rotating	2.0 to 3.0
15	Spring, large heavy-duty	4.5
16	Structural steelwork in buildings	4.0 to 6.0
17	Structural steelwork in bridges	5.0 to 7.0
18	Wire ropes	8.0 to 9.0
19	Highly reliable materials where loading and environmental conditions are not severe	1.3 to 1.5
20	Moderately reliable materials where loading and environmental conditions are not severe	1.5 to 2
21	Ordinary materials where loading and environmental conditions are not severe	2 to 2.5
22	For use with less tried and for brittle materials where loading and average environmental	2.5 to 3
23	For use with materials where properties are not reliable and where loading and environmental conditions are not severe, or where reliable materials are used under difficult and environmental conditions	3.0 to 4.0
24	Impact Forces	3.0 to 6.0
25	Brittle Material	1.0 to 6.0

Table 1: Typical Factor of Safety Range

Factor of Safety Calculator

Various factor of safety calculators are available online to calculate the values of the factor of safety with known ultimate strength and allowable stress values. Let’s take an example to calculate the factor of safety for the following situation:

The yield strength of a ductile material is 240 MPa. If the material is subjected to a loading condition that generates the maximum allowable stress of 140 MPa. Then the factor of safety of that material is 240/140=1.7. However, note that both stress values are in the consistent unit before calculating the factor of safety.

Note that with an increase in the factor of safety, the safety level increases. But, the design cost also increases at the same time. So, engineering judgment must be made following industry codes and guidelines to consider a proper factor of safety.

Free Body Diagram: Definition, Purpose, Examples, Steps

Written by Anu Sharma in Civil,Mechanical,Piping Interface,Piping Stress Analysis,Piping Stress Basics

The concept of a free-body diagram is widely used in engineering and physics. A free-body diagram is a force diagram (a graphic, dematerialized, symbolic representation) that shows the relative magnitude and direction of all forces that act on an object in a specified situation. All forces and moments acting on the object are represented using two-dimensional or three-dimensional representation using the free body diagram or FBD concept. As the forces are vector quantities, FBD is also known as a vector diagram. In this article, we will explore more details about the free body diagram.

Purpose of the Free Body Diagram

The purpose of the free-body diagram is to deconstruct a given problem by using only the necessary information. Students can use this diagram as a reference for setting up the calculations to find unknown variables, for example, force directions, moments, or force magnitudes. Free-Body Diagram allows students to clearly visualize a particular problem in its entirety or closely analyze a particular portion of a more complex problem. So basically, FBD is a very useful aid to visualize and solve engineering problems. Note that, for solving a complex problem, a series of free-body diagrams may be required.

Drawing a Free-Body Diagram

In a Free-Body Diagram, the object is represented by its expression, usually a line, box, or dot. The force vectors that act upon the object are represented by a straight arrow while moments are represented by a curved arrow around their respective axis as shown in the image below where a force is acting at B and a moment acts around A. The force vector indicates the magnitude and direction of each force that is acting upon the object. The direction is normally indicated by degrees from the vertical or the horizontal axis while the magnitude is indicated by the units of force. In the case of an unknown direction of a force or magnitude, the unknown value must be labeled.

In addition, it is common to indicate the various types of forces with letters and distinguish between common ones by using subscripts. In the example problem shown in Fig. 1, weight and tension are represented by W and T, and the normal force and force of friction are represented by F_frict and F_norm. There are no hard rules about how forces are labeled as long as their meaning is clear. Free-Body Diagrams should have a labeled coordinate system and must include all the given dimensions, such as length and angles. Generally, a xy-coordinate system is used; however, when dealing with a problem, that is, in three-dimensional space, an xyz-co-ordinate system is required. Coordinate systems can be placed according to the student’s discretion in order to simplify the solving process, so long as the students are following the right-hand rule.

Types of Forces for Free Body Diagram

In order to identify and label forces of a Free-Body Diagram, one must recognize the various types of forces that they will encounter and must know how these forces will interact with each other in order to calculate them.

Weight:

Any object with a mass is known as weight. It can be shown in pounds or Newton’s (N). If the weight is not given, it can be calculated in Newton (N) by multiplying the mass in kilograms (kg) with the Earth’s gravitational constant (9.8 m/s2).

Normal Force:

According to Newton’s Third Law, every action has an equal and opposite reaction. Due to this law, an object that rests on a surface, that is, an object that is not in free fall has a normal force acting in a perpendicular direction to the surface of the object on which it is resting. In the absence of any additional forces, the magnitude of the vertical component of the normal force is equal to the weight of the object.

Friction Force:

Friction force resists movement and always acts in the opposite direction of the movement or potential movement. It also acts parallel to the surface and is perpendicular to the normal force. The friction force is equal in magnitude to the force that provides the movement until and unless the opposing force exceeds the maximum friction force. The maximum friction force can be calculated by multiplying normal force by the surface coefficient of static friction.

Tension:

This force is the pulling force that is exerted on an object by a rope, chain, or cable. Tension force is continuous from one end to another. Because tension force is always continuous and a rope is flexible, pulleys can be utilized to redirect the rope and by extension, the tension force.

Applied Force:

The applied force is a force that is applied by a person or by some other object.

Free Body Diagram Examples

Now we will explain the FBD concept, using the following free body diagram example problem as shown in Fig. 1.

A 50 kg stationary box must be pulled up a 30-degree inclined by a pulley system. The coefficient of static friction between the box and that incline is 0.25. Assuming there is no friction in the pulley system, what force in Newton’s (N) must be applied to the rope in order to move the box up the incline?

**Fig. 1: Example of Free Body Diagram**

How to draw free body diagram

Step 1: Draw the object with no extra features.

Step 2: Identify the forces acting on the box. The box has mass, so it should also have weight, and a force acting downward. Because the stationary box is on a surface, there is a normal force that acts perpendicular to the surface. Further, attached to the box, there is a rope with tension applied. This tension force will act in the direction of the rope. Since the rope is directly attached to the box and in order to move it up the incline, there will be frictional force impeding movement. This force will then act in the opposite direction, down the incline.

Step 3: Add the forces to the image of the object and label the directions of forces in degrees from the vertical or horizontal axis as understood by the geometry in the example. Refer to Fig. 2 which shows the above 3 steps.

Step 4: Label all the known values. At this point, weight is known, that is mass (50 kg) multiplied by gravitational constant (9.8 m/s2). The FBD now contains all the given, important information.

Step 5: As a general rule, the Free-Body Diagram has to be oriented, so that the direction of movement is along with one of the principal axes. In this example, the entire diagram could be reoriented by rotating it to 30° counter-clockwise. This step results in the direction of movement that occurs along the x-axis, and this results in three of the four forces that also get oriented along the x or y-axis. Fig. 3 shows Steps 4 & Step 5.

**Fig. 3: Steps for Drawing a Free Body Diagram**

Solving the Free-Body Diagram

To solve the problem, the force on the rope required to move the box up the incline should be found. This is called the tension force. Finding this force requires a system of equations. As there is currently one known variable, the weight, there are three unknown variables also; therefore, three equations are required. These equations establish a relationship between all of the forces and are required in order to solve for each force.

In this system of equations, the first one creates a relationship between normal force and frictional force. Since the box will not move until the tension force overcomes the frictional force, the maximum frictional force is needed. The maximum frictional force is equal to the normal force multiplied by the surface coefficient of static friction, that is 0.25, so the first equation will be: F_norm * 0.25 = F_frict

As the question refers to the minimum force required to begin moving the object, the system will be in static equilibrium before the time of movement. When a system that is in static equilibrium is concerned, there are two equations that are formed: ∑F_x=0 and ∑F_y=0, or, the sum of all the forces in the y and x-direction should be equal to zero.

When all forces in each direction are summed up, it is noted that any force that acts along either the x or y-axis (in this case tension, frictional and normal force) will only be present in that axis equation. However, weight does not act along one axis, and therefore, should be broken down into its component parts. This we get by using trigonometric functions. In this case, since the weight acts at a 60-degree angle, the vertical component will be Sin 60 degrees * W, and the horizontal component will be Cos 60 degrees * W.

To achieve the final two equations, the components of the various forces will be added together that act on each axis. Because of the direction of the positive x and y-axis chosen in the previous step, forces on the x-axis which is acting to the left will be negative, whereas forces that are acting to the right will be positive. Likewise, forces on the y-axis which is acting downwards will be negative, and forces that are acting upwards will be positive. Looking at the FBD, three forces will act in the x-direction: the tension force, the horizontal component of the weight, and the frictional force, and two forces will act in the y-direction: the vertical component of the weight and the normal force. This leads to the final equations as follows:

∑F_x= F_frict+cos(60°)*W–T = 0 or F_frict + cos(60°)*W=T

∑F_y= F_norm– sin(60°)*W = 0 or F_norm= sin(60°)*W

Now that the system of equations has been found, the unknown variables can be found by using known information, such that the weight is 490 Newton. Then Equations are combined in order to solve the tension. F_norm=sin (60°)*490 N = 424.4 N

424.4 N*0.25 =F_frict= 106.1 N

106.1 N+cos(60°)*490=T = 351.1 N

With tension force found, the answer to the problem is 351.1 N, that is, this amount of force should be applied to the rope in order to move the box up the incline.

In a similar way, most physics or engineering problems can be simplified, visualized, and solved by drawing a free-body diagram of the problem. If there is more than one object then a free-body diagram of each object can be generated.

Flexible Metal Hoses: An essential guide

Written by Anup Kumar Dey in Engineering Materials,Mechanical,Piping Design Basics,Piping Interface,Piping Stress Analysis,Piping Stress Basics

A flexible hose is a type of piping used to connect two distant points to transport or transfer fluid. In Oil & Gas applications, hoses are used when there is a considerable relative movement. A variety of fluids and fluidized solids can easily be transferred through flexible hoses to other locations. These are most commonly known as hosepipes. Along with loading and unloading services in processing plants, these are widely used by homeowners as garden hoses. Normal Flexible hoses are made of non-metals like soft plastic material or synthetic rubber. However, flexible hoses of chemical industries that are designed to absorb pipe movements are made of metallic materials.

Non-metallic Flexible Hoses

Flexible hoses are made by extrusion or vulcanization process. To add strength to the non-metallic flexible hoses, they are reinforced using a crisscrossed grid of fibers combined together through braiding, spiraling, or knitting. These reinforced hoses can be long enough. Basically, flexible hoses have four parts; inner tube, reinforcement, End fittings, and protective outer cover.

Flexible Metal Hoses

Metallic flexible hoses consist of corrugated tubing, braid, braid collars, and end-fittings as shown below:

Metallic flexible hoses are available in various end connections like welded pipe ends, flanged ends, threaded ends, tube ends, coupling ends, etc to meet a broad range of application requirements.

**Fig. 2: Flexible Hose End Connections**

Types of Metallic Flexible Hoses

Two types of metallic flexible hoses are widely used in industries.

Corrugated hoses and
Interlocked hoses

Fig. 3 below shows the basic construction of corrugated and interlocked flexible hoses.

**Fig. 3: Corrugated vs Interlocked flexible hoses**

Corrugated Hose:

A corrugated hose is constructed with a bellow of very long length. Fundamentally, the behavior of a corrugated flexible hose is the same as the bellow expansion joint. The flexible hose has to resist the hoop pressure stress, but cannot sustain the longitudinal pressure stress. Also, it has a tendency to squirm under internal pressure. To resist the longitudinal pressure stress and prevent squirm, corrugated hoses are often constructed with braids wrapping around the outside surface as shown in Fig. 4. The braided cover also protects the corrugation from scratch and wear. The braided hose, similar to a tied expansion joint, cannot accommodate any axial movement. On the other hand, the un-braided hose can sustain very small internal pressure.

Due to the lack of a limiting mechanism, a corrugated flexible hose is prone to abuse. It should not be bent beyond its acceptable range. For braided hoses, the situation is even more critical.

As the corrugations are not visible from the outside, a braided hose does not show immediately when damaged. Therefore, for manual handling in such situations as loading/unloading and switching operations corrugated hose is not suitable. The corrugated flexible hose has a continuous metal wall thus making it pressure-tight. It is suitable for handling any type of gas and liquid as long as it is compatible with the hose material.

**Fig. 4: Unbraided and braided flexible hose**

Interlocked Hose:

An interlocked hose is constructed with links that are kept tight with packing material. There are clearances provided between the links that afford the capability of accommodating some axial movement. As the hose is being bent, the clearances gradually close. The hose becomes stiff and cannot bend any further at a certain point when the clearances are completely closed. This sudden stiffening effect serves as a warning to the handler, preventing the interlocked hose from being over-bent. This automatic warning feature makes the interlocked hose especially suitable for manual handling.

The packing mechanism at the interlocked links does not offer a perfect seal. Therefore, the interlocked hose is satisfactory for carrying low-pressure air, steam, and water, but is generally not suitable for conveying gases and “searching” liquids such as kerosene and alcohol. The outside of the interlocked hose is relatively smooth, making it easy to handle without any covering.

Stress Analysis Consideration for Flexible Hoses

The flexible hose assembly is normally not analyzed. In most situations, the end displacements from piping or equipment connections are calculated from p i p e stress analysis software and those values are transferred to the vendor for their consideration. Accordingly, the hose length and installation space are determined.

Pipe Supporting for optimum flexible hose working

A piping system that utilizes a flexible metal hose to absorb pipe movement must be properly anchored and guided to assure correct functioning and maximum service life of the metal hose assembly. The following basic principles should be observed:

The direction of pipe motion must be perpendicular to the centerline (axis) of the hose.
To prevent torsional stress, the pipe shall be anchored at each change of direction where a flexible metal hose is employed. Typical examples of correct and incorrect guiding are shown below in Fig. 5.

Installation considerations for Flexible Hoses

Flexible Hoses are used to accommodate piping and equipment displacements. Hoses are extremely flexible, installations are very easy. However, a few general precautions should be exercised during installation to avoid hose failures.

The hose should not be subjected to twisting; Also, the installation should be such that flexing takes place only in the plane of bending.
The length of the hose should be sufficient to accommodate the offset and movement
The installation space should be adequate to accommodate the length.
Sharp bends should be avoided while installing flexible hoses. The Technical Data Section of the vendor catalog should be followed to maintain the minimum centerline bend radius for intermittent flexing.

While installing flexible hoses, the allowable minimum bend radius is the most fundamental limitation. For interlocked hoses, the limiting radius depends largely on the clearances between links. It has less to do with stress and fatigue, so it generally has only one limiting radius for all applications. For corrugated hoses, on the other hand, the limiting radius depends on the stress at the corrugations.

For pressure hoses with braided reinforcement, the corrugation stress comes mainly from the bending of the hose. Therefore, the corrugation stresses can be controlled by setting a limitation on the bending. In other words, the installation is acceptable if the hose is not bent beyond the limiting radius. Similar to the situation discussed in the bellow expansion joint, the mode of failure of the hose corrugation is due to fatigue. Therefore, the bend radius limitation depends also on the number of operating cycles expected. Most manufacturers provide two limiting radii, one for static applications involving a one-time fit-up installation, and the other for operational movement involving many cycles of intermittent flexing. The whole design and installation process actually ensures that this minimum radius is maintained during the initial layout and throughout the operation.

Factors for Metallic Flexible Hose Selection

The main factors that should be considered while selecting a flexible hose are:

Design and maximum working pressure.
Maximum service temperature of the material.
Fluid flow velocity
Axial, Angular, Offset, Radial, and unpredictable displacements if any.
Vibration tendency if any.
Required cycle/service life.

Materials for Metallic Flexible Hoses

The most common materials used for metallic flexible hoses are:

Carbon Steel
Stainless Steel
Bronze
Monel
Inconel
Copper
Brass
Aluminum
Aluminized Fiberglass
Silicone coated fiberglass

Depending on the operating service temperature range, these materials are decided.

Codes and Standards for Flexible hoses

The codes and standards used for design guidance are listed below:

The Society of Automotive Engineers (SAE) SAEJ513: Requirements for Hydraulic hoses.
ISO 10807: Corrugated flexible metallic hose assemblies for the protection of electrical cables in explosive atmospheres
Interlocked hoses are manufactured from a helically (spiral) wound and overlapping profiled strip in accordance with BS EN ISO 15465.
Pressure equipment directive (PED 97/23/EG)
DIN EN 14585-1: Pipework-Corrugated metal hose assemblies for pressure applications
EN 12434: Cryogenic vessels – cryogenic flexible hoses
DIN EN ISO 10380: Pipework-Corrugated metal hoses and metal hose assemblies
ISO 10806: Pipework – Fittings for corrugated metal hoses
ISO 21969: High-pressure flexible connections for use with medical gas systems
EN 2827: Hose assemblies of stainless steels for chemical products
DIN 3384: Stainless steel flexible hose assemblies for gas applications-safety requirements, testing, marking
EN 14800: Corrugated safety metal hose assemblies for the connection of domestic appliances using gaseous fuels

Applications of Flexible Hoses

Specific applications of flexible hoses include the following:

to water plants or to convey water to a sprinkler (Garden hose).
to water crops in agriculture (tough hose) for drip irrigation.
to convey water to the site of the fire for firefighting service (fire hose).
to carry air from a surface compressor (Air hose) or from air tanks.
In chemistry and medicine, flexible hoses are used to move liquid chemicals or gases around.
A fuel hose carries fuel.
to move liquids under high pressures in the oil industry.
For Heat Tracing
For Auto heater tubing, Ventilating ducting, Moderate suction lines, Automotive exhaust, Dust collecting Ducting, Air Blower ducting, Wiring conduit, Refrigeration tubing armor, Carburetor air intake, hot ash granulate, etc

Data required for ordering a flexible hose

The following data must be supplied while ordering a flexible hose:

Size of hose and connected fittings
Design & Operating temperature
Design and Operating Pressure
Displacements
Service and Application
End-fitting attachment type
Developed Assembly length

All flexible hoses are subject to aging and their performance deteriorates after a number of years. So flexible hoses must be inspected following a company-approved inspection plan or as per manufacturer recommendation.

Recent Posts